Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Задача выполнимости булевых формул23 января 2011Оглавление: 1. Задача выполнимости булевых формул 2. Вычислительная сложность Задача выполнимости булевых формул — важная для теории вычислительной сложности алгоритмическая задача. Экземпляром задачи SAT является булева формула, состоящая только из имен переменных, скобок и операций Согласно теореме Кука, доказанной Стивеном Куком в 1971-м году, задача SAT для булевых формул, записанных в конъюнктивной нормальной форме, является NP-полной. Требование о записи в конъюнктивной форме существенно, так как, например, задача SAT для формул, представленных в дизъюнктивной нормальной форме, тривиально решается за линейное время от размера записи формулы. Точная формулировкаЧтобы четко сформулировать задачу распознавания, необходимо условиться об алфавите, с помощью которого задаются экземпляры языка. Этот алфавит должен быть фиксирован и конечен. В своей книге Хопкрофт, Мотвани и Ульман предлагают использовать следующий алфавит: {« При использовании такого алфавита скобки и операторы записываются естественным образом, а переменные получают следующие имена: x1, x10, x11, x100 и т. д., согласно их номерам, записанным в двоичной системе счисления. Пусть некоторая булева формула, записанная в обычной математической нотации, имела длину N символов. В ней каждое вхождение каждой переменной было описано хотя бы одним символом, следовательно, всего в данной формуле не более N переменных. Значит, в предложенной выше нотации каждая переменная будет записана с помощью Например, формула Просмотров: 1988
|
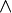 ,
, 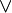 и
и  . Задача заключается в следующем: можно ли назначить всем переменным, встречающимся в формуле, значения ложь и истина так, чтобы формула стала истинной.
. Задача заключается в следующем: можно ли назначить всем переменным, встречающимся в формуле, значения ложь и истина так, чтобы формула стала истинной.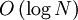 символов. В таком случае, вся формула в новой нотации будет иметь длину
символов. В таком случае, вся формула в новой нотации будет иметь длину 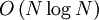 символов, то есть длина строки возрастет в полиномиальное число раз.
символов, то есть длина строки возрастет в полиномиальное число раз.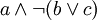 примет вид
примет вид 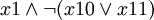 .
.