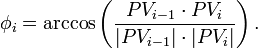Интернет магазин китайских планшетных компьютеров

Компьютеры - Задача о принадлежности точки многоугольнику - Метод суммирования углов

Можно определить, что точка P находится внутри многоугольника c вершинами V₀, V₁, ..., V_n = V₀, вычислив сумму:

,

где φ_i — угол между лучами PV_{i - 1} и PV_i, т.е.:

Можно доказать, что эта сумма есть не что иное, как winding number точки P относительно границы многоугольника, с точностью до константного множителя 2π. Поэтому можно считать, что точка лежит снаружи многоугольника, если сумма равна нулю. Однако данный метод весьма непрактичен, так как требует вычисления дорогостоящих операций для каждого ребра, и был даже назван «худшим в мире алгоритмом» для данной задачи.

К. Вейлером был предложен практичный вариант этого метода, избегающий дорогостоящих операций и приближенных вычислений. Было показано, что сумму углов можно вычислить, используя лишь операцию классификации точки многоугольника по квадрантам относительно точки P. Алгоритм Вейлера и некоторые улучшения к нему описываются в .
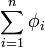