Компьютеры - Задача классификации - Математическая постановка задачи23 января 2011
Оглавление:
1. Задача классификации
2. Математическая постановка задачи
3. Типология задач классификации
Пусть 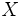 — множество описаний объектов, — множество описаний объектов, 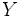 — множество номеров классов. Существует неизвестная целевая зависимость — отображение — множество номеров классов. Существует неизвестная целевая зависимость — отображение 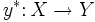 , значения которой известны только на объектах конечной обучающей выборки , значения которой известны только на объектах конечной обучающей выборки 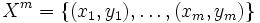 . Требуется построить алгоритм . Требуется построить алгоритм 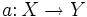 , способный классифицировать произвольный объект , способный классифицировать произвольный объект 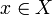 . .
Вероятностная постановка задачи
Более общей считается вероятностная постановка задачи. Предполагается, что множество пар «объект, класс» 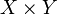 является вероятностным пространством с неизвестной вероятностной мерой является вероятностным пространством с неизвестной вероятностной мерой 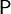 . Имеется конечная обучающая выборка наблюдений . Имеется конечная обучающая выборка наблюдений 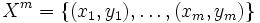 , сгенерированная согласно вероятностной мере , сгенерированная согласно вероятностной мере 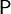 . Требуется построить алгоритм . Требуется построить алгоритм 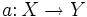 , способный классифицировать произвольный объект , способный классифицировать произвольный объект 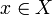 . .
Признаковое пространство
Признаком называется отображение 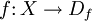 , где , где 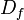 — множество допустимых значений признака. Если заданы признаки — множество допустимых значений признака. Если заданы признаки 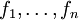 , то вектор , то вектор 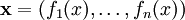 называется признаковым описанием объекта называется признаковым описанием объекта 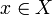 . Признаковые описания допустимо отождествлять с самими объектами. При этом множество . Признаковые описания допустимо отождествлять с самими объектами. При этом множество 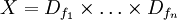 называют признаковым пространством. называют признаковым пространством.
В зависимости от множества Df признаки делятся на следующие типы:
- бинарный признак: Df = {0,1};
- номинальный признак: Df — конечное множество;
- порядковый признак: Df — конечное упорядоченное множество;
- количественный признак: Df — множество действительных чисел.
Часто встречаются прикладные задачи с разнотипными признаками, для их решения подходят далеко не все методы.
Просмотров: 3666
|
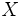 — множество описаний объектов,
— множество описаний объектов, 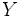 — множество номеров классов. Существует неизвестная целевая зависимость — отображение
— множество номеров классов. Существует неизвестная целевая зависимость — отображение 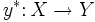 , значения которой известны только на объектах конечной обучающей выборки
, значения которой известны только на объектах конечной обучающей выборки 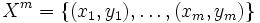 . Требуется построить алгоритм
. Требуется построить алгоритм 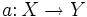 , способный классифицировать произвольный объект
, способный классифицировать произвольный объект 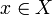 .
.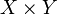 является вероятностным пространством с неизвестной вероятностной мерой
является вероятностным пространством с неизвестной вероятностной мерой 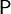 . Имеется конечная обучающая выборка наблюдений
. Имеется конечная обучающая выборка наблюдений 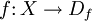 , где
, где 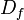 — множество допустимых значений признака. Если заданы признаки
— множество допустимых значений признака. Если заданы признаки 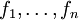 , то вектор
, то вектор 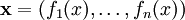 называется признаковым описанием объекта
называется признаковым описанием объекта 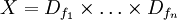 называют признаковым пространством.
называют признаковым пространством.