Интернет магазин китайских планшетных компьютеров

Компьютеры - Выделение границ - Подходы к выделению границ

Существует множество подходов к выделению границ, но практически все можно разделить на две категории: методы, основанные на поиске максимумов, и методы, основанные на поиске нулей. Методы, основанные на поиске максимумов, выделяют границы с помощью вычисления «силы края», обычно выражения первой производной, такого как величина градиента, и затем поиска локальных максимумов силы края, используя предполагаемое направление границы, обычно перпендикуляр к вектору градиента. Методы, основанные на поиске нулей, ищут пересечения оси абсцисс выражения второй производной, обычно нули Лапласиана или нули нелинейного дифференциального выражения, как будет описано далее. В качестве шага предобработки к выделению границ практически всегда применяется сглаживание изображения, обычно фильтром Гаусса.

Опубликованные методы выделения границ отличаются применяемыми фильтрами сглаживания и способами, как считается сила края. Хотя многие методы выделения границ основываются на вычислении градиента изображения, они отличаются типами фильтров, применяемых для вычисления градиентов в x- и y-направлении.

Выделение границ Канни

Канни изучил математическую проблему получения фильтра, оптимального по критериям выделения, локализации и минимизации нескольких откликов одного края. Он показал, что искомый фильтр является суммой четырех экспонент. Он также показал, что этот фильтр может быть хорошо приближен первой производной Гауссианы. Канни ввел понятие Non-Maximum Suppression, которое означает, что пикселями границ объявляются пиксели, в которых достигается локальный максимум градиента в направлении вектора градиента.

Хотя его работа была проведена на заре компьютерного зрения, детектор границ Канни до сих пор является одним из лучших детекторов. Кроме особенных частных случаев трудно найти детектор, который бы работал существенно лучше, чем детектор Канни.

Детектор Канни-Дерише был выведен из похожего математического критерия, как и детектор Канни, хотя, отталкиваясь от другой точки зрения, он привел к набору рекурсивных фильтров для сглаживания изображения вместо экспоненциальных фильтров и фильтров Гаусса.

Другие методы первого порядка

Для того, чтобы оценить величину градиента изображения или его сглаженной версии, можно применить различные операторы градиента. Простейший подход — использовать центральные разности:

соответствующие применению следующих фильтров к изображению:

Хорошо известный оператор Собеля основывается на следующих фильтрах:

Получив такие оценки, мы можем вычислить величину градиента следующим образом:

а направление градиента вычисляется так:

Другие операторы для вычисления градиента изображения были предложены Прюиттом и Робертсом.

Выделение порогом и объединение

После того, как мы нашли силу границы, следующий шаг — применить порог, чтобы решить находится или нет граница в данной точке изображения. Чем меньше порог, тем больше границ будет находиться, но тем более восприимчивым к шуму станет результат, выделяя лишние данные изображения. Наоборот, высокий порог может пропустить слабые края или получить границу фрагментами.

Если порог применяется просто к изображению величины градиента, полученные границы будут толстыми и потребуется некоторая постобработка, делающая край тонким и точным. Если же выделить границы с помощью Non-Maximum Suppression, границы будут тонкими по определению и их можно будет соединить в полигоны процедурой соединения краев. На дискретной сетке этап подавления немаксимумов может быть реализован с помощью оценки направления градиента, используя первые производные, округление направления на значения с шагом 45 градусов и, наконец, сравнении значений градиента в полученном направлении градиента.

Традиционным подходом к решению проблемы нахождения подходящего порога являются пороги «с запозданием». Метод использует несколько порогов. Мы используем верхний порог, чтобы найти точку начала границы. После того, как мы получили стартовую точку, мы отслеживаем границу, точка за точкой, пока значение силы края выше нижнего порога. Этот алгоритм подразумевает, что границы — это скорее всего непрерывные кривые, и позволяет нам прослеживать слабые участки границ без допущения того, что все шумные точки на изображении будут помечены как края. Однако, у нас все ещё есть проблема выбора подходящих значений порогов для этого метода, так как оптимальные параметры могут меняться от изображения к изображению.

Уточнение границы

Уточнение границы — процесс, который делает границы тонкими, удаляя нежелательные ложные точки, которые появляются на границе. Эта техника применяется уже после того, как изображение было сглажено, был применен оператор границ для вычисления силы края и после того, как границы были очищены используя подходящие пороги. Этот метод удаляет все нежелательные точки и при аккуратном применении выдает границы толщиной в один пиксель.

Плюсы:

• резкие и тонкие границы позволяют повысить эффективность распознавания объектов
• при использовании трансформации Хафа для обнаружения прямых или эллипсов, тонкие границы дают значительно лучшие результаты
• если граница представляет собой границу некоторой области, тонкие границы позволяют вычислить такие параметры, как периметр, без какой-то сложной арифметики

Существует много популярных методов для решения этой задачи. Один из них описан далее:

1. Выбрать тип связности: 8, 6 или 4
   • Предпочтительна 8-связность, при которой рассматриваются все пиксели, непосредственно окружающие текущий пиксель
2. Удалить точки сверху, снизу, слева и справа от точки
   • Делать это следует в несколько проходов, то есть сначала удалить точки в одном направлении, затем на обработанном изображении удалить точки на другом.
   • Точка удаляется в следующем случае:
     1. У этой точки нет соседей сверху
     2. Эта точка не является концом линии
     3. Удаление этой точки никак не повлияет на связанность её соседей
     4. ИЛИ это изолированная точка
   • Иначе, точка не удаляется
3. Предыдущий шаг можно повторять несколько раз, в зависимости от желаемого уровня «аккуратности» границы.

Подходы второго порядка к выделению границ

Некоторые операторы выделения границ вместо работы с градиентом используют вторые производные яркости изображения. Это естественным образом определяет силу изменения градиента. Таким образом, в идеальном случае, обнаружение нулей второй производной позволит обнаружить локальные максимумы градиента.

Оператор Марра-Хилдрета основан на вычисления корней оператора Лапласа, примененного к изображению, сглаженному фильтром Гаусса. Однако, было показано, что этот оператор выделяет ложные границы на однородных участках изображения, где градиент имеет локальный минимум. К тому же этот оператор плохо локализовывал скругленные края. Поэтому данный оператор представляет сейчас скорее историческую ценность.

Дифференциальное выделение границ

Более продвинутый способ выделения границ второго порядка, который так же выделяет границы с пиксельной точностью, — использование следующего дифференциального подхода к обнаружению нулей второй производной по направлению вектора градиента.

Введем в каждой точке изображения локальную систему координат , где v-направление параллельно градиенту. Предполагая, что изображение было сглажено фильтром Гаусса, и масштабного представление L на масштабе t было посчитано, мы можем потребовать, чтобы величина градиента масштабного представления, которое равно первой производной по направлению L_v в v-направлении, будет иметь первую производную в v-направлении, равную нулю

,

в то время как вторая производная в v-направлении от L_v должна быть отрицательной, так как на интересуют только максимумы, то есть:

.

Записанное в качестве явного выражения от локальных частных производных L_x, L_y … L_yyy, данное определение края может быть выражено в качестве нулевых линий дифференциального инварианта

который удовлетворяет следующему условию:

где L_x, L_y … L_yyy обозначают частные производные посчитанные на масштабном представлении L, полученном с помощью фильтрации исходного изображения фильтром Гаусса.

В данном случае края будут автоматически представлять собой непрерывные кривые с пиксельной точностью. К полученным краям может быть дополнительно применено выделение с помощью порогов с запозданием.

На практике, первые производные могут быть посчитаны так, как описывалось ранее, в то время как вторые производные могут быть вычислены из масштабного представления L так:

соответствуя следующим операторам:

Производные более высоких порядков могут быть посчитаны аналогично.

Подходы, основанные на согласованности фаз

Последнее развитие техник выделения границ использует частотный подход для обнаружения границ. Методы использующие согласованность фаз пытаются найти области на изображении, где все синусоиды в частотном пространстве находятся в фазе. Эти области обычно будут соответствовать областям воспринимаемой границы, независимо от того, насколько сильное там изменение яркости. Ключевое преимущество данного метода заключается в том, что он сильно выделяет «ленты Маха» и позволяет избежать типичных ложных границ вокруг грубого края.
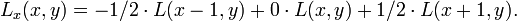
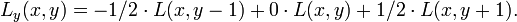
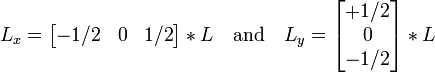
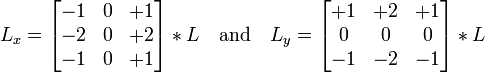
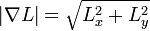
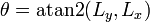
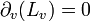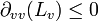