|
|
|
23 января 2011
Оглавление:
1. Вейвлеты Добеши
2. Ортогональные нормированные коэффициенты добеши низких порядков
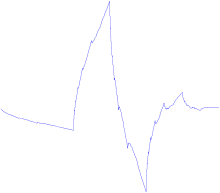
Вейвлет Добеши порядка 2
Вейвлеты Добеши — семейство ортогональных вейвлетов с компактным носителем, вычисляемым итерационным путем. Названы в честь математика из США, первой построившей данное семейство, Ингрид Добеши.
Построение вейвлетов Добеши
Для построения вейвлетов воспользуемся уравнением растяжения и вейвлет-уравнением
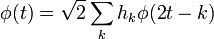
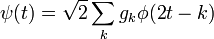
Компактность носителя функций φ и ψ может быть достигнута, если будет выбрано конечное число 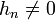 таким образом, чтобы была достигнута ортогональность и гладкость вейвлета, либо чтобы выполнялось условие моментов. Для области Фурье условие ортогональности и гладкости выглядит следующим образом: таким образом, чтобы была достигнута ортогональность и гладкость вейвлета, либо чтобы выполнялось условие моментов. Для области Фурье условие ортогональности и гладкости выглядит следующим образом:
| m0 | + | m0 | = 1, где 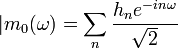 — тригонометрический полином, — тригонометрический полином,
при условии моментов 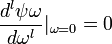 ,для ,для 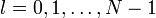
принимающий вид:

Если положить, что M0 = m0 | — полином по cos, то условие нулевых моментов дает 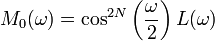 , где , где 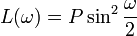 — полином по cos — полином по cos
Для поиска коэффициентов hn необходимо получить m0, выделив форму полинома P. Из условия ортогональности и условия нулевых моментов следует, что
P =)
Разложив до порядка N − 1, получим явный вид полинома:
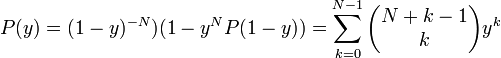
Путем спектрального разложения на множители можно извлечь корни m0 из P:
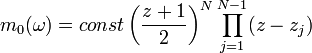
Искомые коэффициенты вейвлета 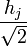 будут являться коэффициентами при z в обратном порядке. будут являться коэффициентами при z в обратном порядке.
Просмотров: 3618
|

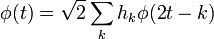
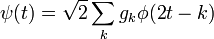
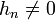 таким образом, чтобы была достигнута ортогональность и гладкость вейвлета, либо чтобы выполнялось условие моментов. Для области Фурье условие ортогональности и гладкости выглядит следующим образом:
таким образом, чтобы была достигнута ортогональность и гладкость вейвлета, либо чтобы выполнялось условие моментов. Для области Фурье условие ортогональности и гладкости выглядит следующим образом: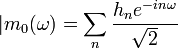 — тригонометрический полином,
— тригонометрический полином,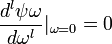 ,для
,для 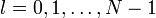

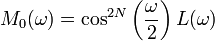 , где
, где 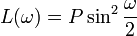 — полином по cos
— полином по cos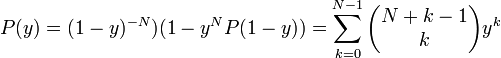
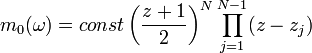
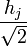 будут являться коэффициентами при z в обратном порядке.
будут являться коэффициентами при z в обратном порядке.