Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Вейвлет Койфлет - Вейвлеты Р. Койфмана — койфлеты22 января 2011Оглавление: 1. Вейвлет Койфлет 2. Вейвлеты Р. Койфмана — койфлеты 3. Преимущества и пременение койфлетов Вейвлеты Добеши и койфлеты индуцируются общей 2π -периодической функцией Теорема. В том случае, если функция принадлежит пространству Соболева и при этом ядро аппроксимации удовлетворят некоторому условию моментов, тогда аппроксимация данной функции обладает наперед заданной точностью. Обратно: для аппроксимации, обладающей известной сходимостью, ядро аппроксимации удовлетворяет некоторому условию моментов. Для построения вейвлетов Добеши и койфлетов рассмотрим функцию m0 :
где L — тригонометрический полином. Для построения койфлетов потребуем выполнение следующих условий: Или в частотной области:
Если существует некоторое число
где
F — тригонометрический полином, выбираемый так, чтобы выполнялось условие:
Просмотров: 3674
|
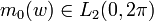 , но для койфлетов к ней добавляется набор условий, определяющих равенство нулю моментов соответствующей скейлинг-функции, что весьма полезно в задачах аппроксимации.
, но для койфлетов к ней добавляется набор условий, определяющих равенство нулю моментов соответствующей скейлинг-функции, что весьма полезно в задачах аппроксимации.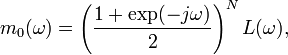
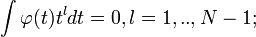
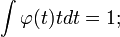
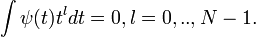
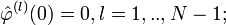
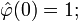
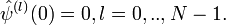
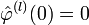 подразумевает m = 0,l = 1,..,N − 1;.
подразумевает m = 0,l = 1,..,N − 1;.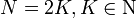 , тогда, согласно работе рассматриваемая функция m0 для койфлетов может быть представлена в виде:
, тогда, согласно работе рассматриваемая функция m0 для койфлетов может быть представлена в виде: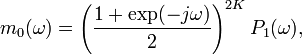
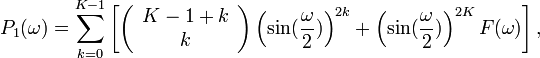
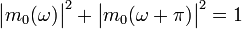 .
.