Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Вейвлет Койфлет22 января 2011Оглавление: 1. Вейвлет Койфлет 2. Вейвлеты Р. Койфмана — койфлеты 3. Преимущества и пременение койфлетов 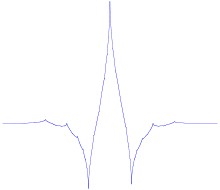
Вейвлет Койфлет порядка 1
К вейвлет-функциям с компактным носителем относятся вейвлеты Добеши, койфлеты и симмлеты. Метод построения вейвлет-функций с компактным носителем принадлежит Ингрид Добеши. Койфлеты являются частным случаем вейвлетов Добеши с нулевыми моментами скейлинг-функции. Основные положения теории вейвлет-функцийортонормированный базис в L2. С помощью вейвлет-анализа можно выделить высокочастотные всплески, например, в эксперементальных данных. В отличие от анализа Фурье, применяемого в этих же целях, вейвлет-анализ позволяет выявить не только частотную составляющую информации, но и ее временную локализацию. Преимущества вейвлетов заключаются и в том, что для задачи приближения число спектральных коэффициентов много меньше числа спектральных коэффициентов Фурье. Это свойство используется в алгоритмах сжатия данных. Например, при одинаковом уровне сжатия по алгоритму JPEG и вейвлет-алгоритму, после восстановления, второй дает гораздо лучшее качество картинки . Построение систем вейвлет-функцийОпределение скейлинг-функцииПусть
образует ортогональный базис в L2. Введем
Пусть
Далее, пусть
Определение. Пусть Определение. Если Определение материнской вейвлет-функцииПусть последовательность пространств
или же:
Построим материнскую вейвлет-функцию Вейвлет-разложениеТаким образом, согласно и определению функций
при этом коэффициенты ряда вычисляются следующим образом:
Коэффициенты αk дают информацию об общей форме исследуемой функции, тогда как коэффициенты Уровень разложения задается числом пространств Wj используемых для анализа. Функция m0Утверждение. Пространства Vj являются вложенными
где Лемма 0.Система функций
где
m0 = 0. Просмотров: 3673
|
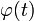 представляет собой функцию из в L2, такую что множество ее трансляций
представляет собой функцию из в L2, такую что множество ее трансляций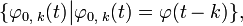
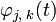 согласно:
согласно: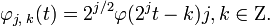
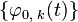 — ортонормированный базис пространства V0. Тогда для любой функции
— ортонормированный базис пространства V0. Тогда для любой функции 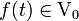 :
: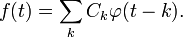
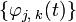 — ортонормированный базис пространства Vj ,
— ортонормированный базис пространства Vj , 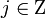 . Тогда мы получаем последовательность пространств
. Тогда мы получаем последовательность пространств 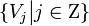 , таких что
, таких что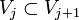 .
.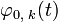 — ортонормированный базис в L2, тогда разложение функции
— ортонормированный базис в L2, тогда разложение функции 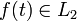 по базисам пространств
по базисам пространств 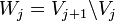 . Тогда
. Тогда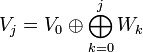 ,
,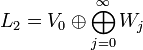 .
. 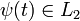 ортогональную скейлинг-функции
ортогональную скейлинг-функции 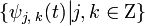 — базис в пространстве Wj.
— базис в пространстве Wj.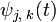 и
и 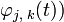 как базисов в соответствующих пространствах, получаем, что любая функция
как базисов в соответствующих пространствах, получаем, что любая функция 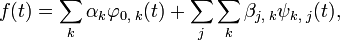
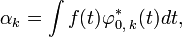
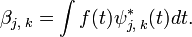
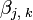 содержат информацию о деталях общей формы.
содержат информацию о деталях общей формы.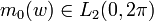 такая, что
такая, что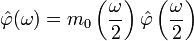 ,
, 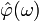 -Фурье-образ функции
-Фурье-образ функции 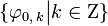 является ортонормированной в L2 тогда и только тогда, когда
является ортонормированной в L2 тогда и только тогда, когда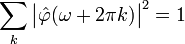 .
.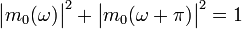 .
.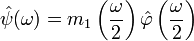 ,
, 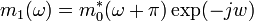 — вейвлет-функция.
— вейвлет-функция.