Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Вейвлет Хаара23 января 2011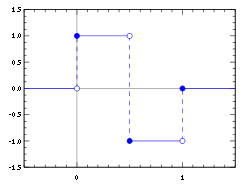
Вейвлет Хаара
Вейвлет Хаара — один из первых и наиболее простых вейвлетов. Он был предложен венгерским математиком Альфредом Хааром в 1909 году. Вейвлеты Хаара ортогональны, обладают компактным носителем, хорошо локализованы в пространстве, но не являются гладкими. Впоследствии Ингрид Добеши стала развивать теорию ортогональных вейвлетов и предложила использовать функции, вычисляемые итерационным путем, названные вейвлетами Добеши. Построение вейвлета ХаараРодительская вейвлет-функция ψ с нулевым значением интеграла
Масштабирующая функция φ с единичным значением интеграла Преобразование ХаараПреобразование Хаара используется для сжатия входных сигналов, компрессии изображений, в основном цветных и черно-белых с плавными переходами. Идеален для картинок типа рентгеновских снимков. Данный вид архивации известен довольно давно и напрямую исходит из идеи использования когерентности областей. Степень сжатия задается и варьируется в пределах 5-100. При попытке задать больший коэффициент на резких границах, особенно проходящих по диагонали, проявляется "лестничный эффект" - ступеньки разной яркости размером в несколько пикселов. Преобразование Хаара для одномерного сигналаПусть имеется одномерный дискретный входной сигнал S. Каждой паре соседних элементов ставятся в соответствие два числа: ПримерПусть входящий сигнал представляется в виде строки из 8 значений яркости пикселов:. После применения преобразования Хаара получаются следующие две последовательности a1 и b1: и. Стоить заметить, что значения b1 достаточно близки к 0. Повторяя операцию, применительно к последовательности a1, получаем:. На примере преобразования Хаара хорошо видна структура дискретного вейвлет-преобразования сигнала. На каждом шаге преобразования сигнал распадается на две составляющие: приближение с более низким разрешением и детализирующую информацию. Преобразование Хаара для двумерного сигналаДвумерное преобразование Хаара — это не что иное, как композиция одномерных преобразований Хаара. Пусть двумерный входной сигнал представляется матрицей S. После применения одномерного преобразования Хаара к каждой строке матрицы S получаются две новые матрицы, строки которых содержат аппроксимированную и детализирующую часть строк исходной матрицы. Аналогично к каждому столбцу полученных матриц применяют одномерное преобразование Хаара и на выходе получают четыре матрицы, одна из которых является аппроксимирующей составляющей исходного сигнала, а три оставшиеся содержат детализирующую информацию — вертикальную, горизонтальную и диагональную. Просмотров: 3310
|
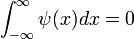 , определяющая детали сигнала, задается следующим образом:
, определяющая детали сигнала, задается следующим образом: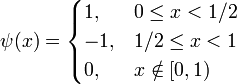
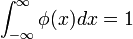 , определяющая грубое приближение сигнала, постоянна:
, определяющая грубое приближение сигнала, постоянна: 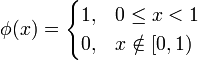
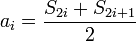 и
и 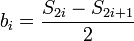 . Повторяя данную операцию для каждого элемента исходного сигнала, на выходе получают два сигнала, один из которых является огрубленной версией входного сигнала — ai, а второй содержит детализирующую информацию, необходимую для восстановления исходного сигнала. Аналогично, преобразование Хаара может быть применено к полученному сигналу ai и тд.
. Повторяя данную операцию для каждого элемента исходного сигнала, на выходе получают два сигнала, один из которых является огрубленной версией входного сигнала — ai, а второй содержит детализирующую информацию, необходимую для восстановления исходного сигнала. Аналогично, преобразование Хаара может быть применено к полученному сигналу ai и тд.