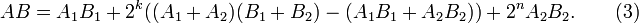Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Умножение Карацубы - Описание метода22 января 2011Оглавление: 1. Умножение Карацубы 2. Описание метода Первый вариантЭтот вариант основан на формуле
Поскольку 4ab = −, то умножение двух чисел a и b эквивалентно по сложности выполнения возведению в квадрат. Пусть X есть n-значное число, то есть где Будем считать для простоты, что
где и находим: Числа X1 и X2 являются k-значными. Число X1 + X2 может иметь k + 1 знаков. В этом случае представим его в виде 2X3 + X4, где X3 есть k-значное число, X4 — однозначное число. Тогда Обозначим где c > 0 есть абсолютная константа. Действительно, правая часть содержит сумму трёх квадратов k-значных чисел, k = n2 , которые для своего вычисления требуют и принимая во внимание, что получаем Тем самым для количества Если же n не является степенью двух, то определяя целое число m неравенствами Все остальные рассуждения остаются в силе и для Второй вариантЭто непосредственное умножение двух n-значных чисел, основанное на формуле
Пусть, как и раньше n = 2, n = 2k, A и B — два n-значных числа. Представляя A и B в виде где Таким образом, в этом случае формула заменяется формулой. Если теперь обозначить символом ЗамечанияОтметим, что представленный выше первый способ умножения можно трактовать как алгоритм вычисления с точностью до n знаков функции y = x в некоторой точке x = x1. Если разбивать X не на два, а на большее количество слагаемых, то можно получать асимптотически лучшие оценки сложности вычисления произведения. Метод умножения Шёнхаге — Штрассена имеет меньшую асимптотическую сложность, чем алгоритм Карацубы. Просмотров: 2753
|
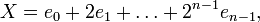
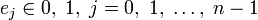 .
.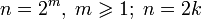 . Представляя X в виде
. Представляя X в виде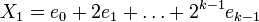
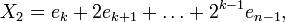
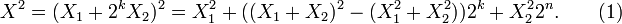
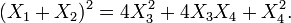
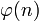 — количество операций, достаточное для возведения n-значного числа в квадрат по формуле. Из следует, что для
— количество операций, достаточное для возведения n-значного числа в квадрат по формуле. Из следует, что для 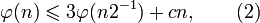
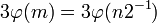 операций. Все остальные вычисления в правой части, а именно умножение на
операций. Все остальные вычисления в правой части, а именно умножение на 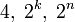 , пять сложений и одно вычитание не более чем 2n-значных чисел требуют по порядку не более n операций. Отсюда следует. Применяя последовательно к
, пять сложений и одно вычитание не более чем 2n-значных чисел требуют по порядку не более n операций. Отсюда следует. Применяя последовательно к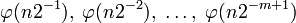

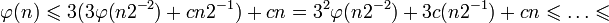
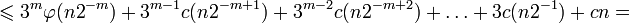
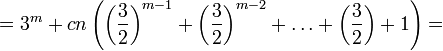

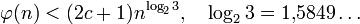
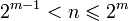 , представим X как 2-значное число, то есть полагаем последние 2 − n знаков равными нулю:
, представим X как 2-значное число, то есть полагаем последние 2 − n знаков равными нулю: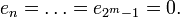

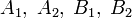 — k-значные числа, находим:
— k-значные числа, находим: