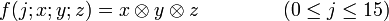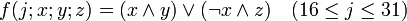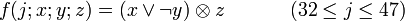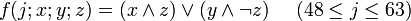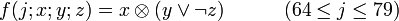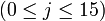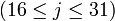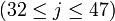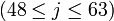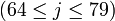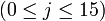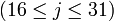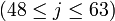Two-Track-MAC - Принцип работы

Интернет магазин китайских планшетных компьютеров

Компьютеры - Two-Track-MAC - Принцип работы

16 июня 2011

Оглавление:
1. Two-Track-MAC
2. Описание
3. Принцип работы
4. Примеры
5. Безопасность
6. Вычислительная эффективность

Как уже отмечалось Two-Track-MAC имеет два параллельных блока преобразований L и R, принимающие на вход сообщение M и ключ K. В результате каждый из блоков работает независимо друг от друга и создает два различных представления одних и тех же данных.

Предположим для начала, что размер сообщения M составляет 512 бит. Размер ключа K всегда фиксирован и составляет 160 бит. Для усложнения преобразований L дает на выходе пять 32-битных слов . Т.е. формально разделяет пока ещё предварительный вариант ключа на 5 частей одинаковых размеров. Аналогично набор дает на выходе функция R. Затем эти слова вычитаются по модулю 2. Это своего рода смешивание двух значений для приведения из к фиксированной длине 160 бит. Окончательный результат: $E = ~~, где <img class=$ . Собственно это и есть то, ради чего все делалось. E является кодом аутентичности сообщения M.

Если сообщение превышает 512 бит, то M разбивается на блоки $~~M = M_1 M_2 M_3...M_n$ , где M_i имеет длину 512 бит. В результате процесс мы все те же операции проводим над каждым блоком, перемешивая их по очереди. Сообщение длиной не кратной 512 дополняется нулями и единицами до нужного нам размера.

Подробнее о смешивании результатов выполнения L и R

После того, как каждая ветвь алгоритма обработает очередной блок сообщения, результаты должны каким то образом преобразоваться так, чтобы на выходе получилась фиксированная длина ключа. Рассмотрим данный процесс более подробно.

Введем обозначения: $A = = L^~~$

$B = = R^~~$

Далее создаем два 160-битных блоков $C =~~$ и $D =~~$ . Эти блоки заполняются различными комбинациями с выходными данными функций L и R. А именно:

$C_2 = A_3 - B_0 ~~$ ,

$C_3 = A_4 - B_1 ~~$ ,

$C_0 = - B_3 ~~$ ,

$C_1 = A_2 - B_4 ~~$ ,

$D_1 = - B_0 ~~$ ,

$D_2 = A_0 - B_1 ~~$ ,

$D_3 = A_1 - B_2 ~~$ ,

$D_4 = A_2 - B_3 ~~$ ,

$D_0 = A_3 - B_4 ~~$ .

Не стоит забывать, что все сложения и вычитания производятся по модулю 2.

Когда сообщение больше 512 бит, полученные блоки C и D будут подаваться на вход вместо ключа для следующего блока сообщения. Так происходит пока мы не пройдем все сообщение.

Условно весь процесс создания создания кода аутентичности можно представляется как :

$~~HL = A = L^{*}$

$~~HR = B = R^{*}$

затем процесс повторяется, с той лишь разницей, что в качестве ключа выступает результат предыдущего вычисления.

$~~->$

$~~HL = A = L^{*}$

$~~HR = B = R^{*}$

На последней итерации получается мы меняем местами входные данные для R и L. Это делается для повышения стойкости кода аутентификации. Окончательные $~~HL$ и $~~HR$ представляют собой Two-track-MAC.

Псевдокод

Ниже представлен псевдокод алгоритма.


FOR i:= 0 TO n-1 {
  
  
  IF FOR j:= 0 TO 79 {
     ;
     
     
     
  }
  else FOR j:= 0 TO 79 {
     
     
     
     
  }
  
  
  
  
  IF {
     
     
     
     
 }
}

;

Пояснения и возможные реализации

Здесь даются пояснения к обозначениям, используемым в псевдокоде TTMAC, а так же обсуждается возможность их реализации.

f - нелинейная функция, работающая с битами. Для различных j производит различные операции над x,y,z. А именно:

$f = x \otimes y \otimes z ~~~~~~~~~~~~~$
$f = \lor~~~$
$f = \otimes z ~~~~~~~~~~$
$f = \lor~~~~$
$f = x \otimes~~~~~~~~~$

Например на языке C удобно представить эти функции в виде макросов :

#define F1       
#define F2    ))
#define F3    )
#define F4    ))
#define F5    )

Символами c,c обозначены константы, значения которых определяется диапазоном j:

с = 00000000x $~~~~~$
с = 5A827999x $~~~~$
с = 6ED9EBA1x $~~~~$
с = 8F1BBCDCx $~~~~~$
с = A953FD4Ex $~~~~$
с' = 50A28BE6x $~~~~$
с' = 5C4DD124x $~~~$
с' = 6D703EF3x $~~~~$
с' = 7A6D76E9x $~~~~$
с' = 00000000x $~~~~$

Функции r и r' дают один из 16 возможных блоков, на которые делится исходное сообщение. Так как блоки имеют размер 512 бит, то r может принимать значения от 0 до 15. Где r = 0 = 0) означает биты 0...15, а r = 15 = 15) - биты 495...511 соответственно.

r = j при $\text{[math]}$
r = 7; 4; 13; 1; 10; 6; 15; 3; 12; 0; 9; 5; 2; 14; 11; 8
r = 3; 10; 14; 4; 9; 15; 8; 1; 2; 7; 0; 6; 13; 11; 5; 12
r = 1; 9; 11; 10; 0; 8; 12; 4; 13; 3; 7; 15; 14; 5; 6; 2
r = 4; 0; 5; 9; 7; 12; 2; 10; 14; 1; 3; 8; 11; 6; 15; 13
r' = 5; 14; 7; 0; 9; 2; 11; 4; 13; 6; 15; 8; 1; 10; 3; 12
r' = 6; 11; 3; 7; 0; 13; 5; 10; 14; 15; 8; 12; 4; 9; 1; 2
r' = 15; 5; 1; 3; 7; 14; 6; 9; 11; 8; 12; 2; 10; 0; 4; 13
r' = 8; 6; 4; 1; 3; 11; 15; 0; 5; 12; 2; 13; 9; 7; 10; 14
r' = 12; 15; 10; 4; 1; 5; 8; 7; 6; 2; 13; 14; 0; 3; 9; 11

Пример: Пусть сообщение:

M = "Software-optimized universal hashing and message authentication."

Поставим в соответствие каждому символу определенный код:

"S", "o", "f", "t", "w", "a", "r", "e", "-", "o", "p", "t", "i", "m", "i", "z"
 83, 111, 102, 116, 119, 97,  114, 101, 45,  111, 112, 116, 105, 109, 105, 122
"e", "d", " ", "u", "n", "i", "v", "e", "r", "s", "a", "l", " ", "h", "a", "s"
101, 100,  32, 117, 110, 105, 118, 101, 114, 115,  97, 108,  32, 104,  97, 115
"h", "i", "n", "g", " ", "a", "n", "d", " ", "m", "e", "s", "s", "a", "g", "e"
104, 105, 110, 103, 32,  97, 110,  100, 32,  109, 101, 115, 115,  97, 103, 101
" ", "a", "u", "t", "h", "e", "n", "t", "i", "c", "a", "t", "i", "o", "n", "."
 32,  97, 117, 116, 104, 101, 110, 116, 105,  99,  97, 116, 105, 111, 110,  46

В двоичном представлении текст сообщение будет содержать 512 нулей и единиц. Затем оно разбивается на 16 блоков по 32 бита:

M₀ =  = 
M₁ =  =
M₂ =  =
M₃ =  = 
M₄ =  = 
M₅ =  =
M₆ =  = 
M₇ =  =
M₈ =  = 
M₉ =  =
M₁₀ =  = 
M₁₁ =  =
M₁₂ =  = 
M₁₃ =  =
M₁₄ =  = 
M₁₅ =  =

В результате функция M) выдаст:. А M₂) даст третий бит, т.е 1.

s и s - дают номер бита для операции битового поворота rol.

s = 11; 14; 15; 12; 5; 8; 7; 9; 11; 13; 14; 15; 6; 7; 9; 8
s = 7; 6; 8; 13; 11; 9; 7; 15; 7; 12; 15; 9; 11; 7; 13; 12
s = 11; 13; 6; 7; 14; 9; 13; 15; 14; 8; 13; 6; 5; 12; 7; 5
s = 11; 12; 14; 15; 14; 15; 9; 8; 9; 14; 5; 6; 8; 6; 5; 12
s = 9; 15; 5; 11; 6; 8; 13; 12; 5; 12; 13; 14; 11; 8; 5; 6
s' = 8; 9; 9; 11; 13; 15; 15; 5; 7; 7; 8; 11; 14; 14; 12; 6
s' = 9; 13; 15; 7; 12; 8; 9; 11; 7; 7; 12; 7; 6; 15; 13; 11
s' = 9; 7; 15; 11; 8; 6; 6; 14; 12; 13; 5; 14; 13; 13; 7; 5
s' = 15; 5; 8; 11; 14; 14; 6; 14; 6; 9; 12; 9; 12; 5; 15; 8
s' = 8; 5; 12; 9; 12; 5; 14; 6; 8; 13; 6; 5; 15; 13; 11; 11

На самом все выше описанные выражения заимствованны из алгоритма хеш-функции RIPEMD-160. Собственно поэтому RIPEMD-160 и является основой для Two-Track-MAC.

Реализация алгоритма TTMAC была включен в криптографическую библиотеку Crypto++® Library.

<<< Trusted Platform Module

UMAC >>>

Компьютерное аппаратное обеспечение
Вычислительные комплексы
Компьютерные данные
Компьютерные журналы
Классы компьютеров
Компьютеры

Программное обеспечение
Производители компьютеров
Профессии в ИТ
Системное администрирование
Компьютерный сленг
Списки компьютерных терминов

Человеко-компьютерное взаимодействие