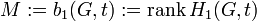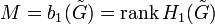Интернет магазин китайских планшетных компьютеров

Компьютеры - Цикломатическая сложность - Описание

Граф управления потоком простой программы. Программа начинает выполняться с красного узла, затем идут циклы. Выход из цикла осуществляется через условный оператор и конечный выход из программы в синем узле. Для этого графа E = 9, N = 8 и P = 1, цикломатическая сложность программы равна 3.

Цикломатическая сложность части программного кода — счётное число линейно независимых маршрутов через программный код. Например, если исходный код не содержит никаких точек решений, таких, как указания IF или циклы FOR, то сложность равна единице, поскольку, есть только единственный маршрут через код. Если код имеет единственный оператор IF, содержащий простое условие, то должно быть два пути через код: один путь через оператор IF с оценкой как TRUE и один — как FALSE.

Математически, цикломатическая сложность структурного программирования — определение с помощью ссылок от базового блока  программы на ориентированный граф и с помощью рёбер между двумя основными блоками, если управление может переходить с первого на второй граф управления потоком программы. Тогда сложность определяется как::

M = E − N + 2P,

где:

M = цикломатическая сложность,

E = количество рёбер в графе,

N = количество узлов в графе,

P = количество компонентов связности.

Сильносвязанный граф управления потоком той же функции, использующийся для вычисления альтернативным путём. Для этого графа E = 10, N = 8 и P = 1, следовательно, цикломатическая сложность программы всё ещё равна 3.

В другой формулировке используется граф, в котором каждая точка выхода соединена с обратной — точкой входа. В этом случае говорят, что граф будет сильносвязанным и цикломатическая сложность программы будет равняться цикломатическому числу этого графа), которое определяется как:

M = E − N + P

Это может рассматриваться как вычисление числа линейно независимых циклов, которые существуют в графе, то есть тех циклов, которые не содержат в себе других циклов. Надо учитывать, что каждая точка выхода из цикла становится точкой входа в него, то есть по крайней мере одна итерация его для каждой точки выхода.

Для простой программы, или подпрограммы, или метода P всегда эквивалентно 1. Цикломатическая сложность может, тем не менее, применяться к некоторым таким программам или подпрограммам, в таком случае P эквивалентен числу программ, о которых идёт речь, как о каждой подпрограмме, проявляющейся как разрозненное подмножество графа.

Может быть показано, что цикломатическая сложность любой структурированной программы с только одной точкой входа и одной точкой выхода эквивалентна числу точек решения, содержащихся в этой программе, плюс один.

Цикломатическая сложность может быть распространена на программу с многочисленными точками выхода; в этом случае она равна:

π — s + 2

где:

π — число точек решения в программе,

s — число точек выхода.

Формальное определение

Формально, цикломатическая сложность, может быть, определена, как относительное число Бетти, как размер относительнооднородной группы:

Это читается, как «первый однородный граф G, относительно терминального узла t». Этот технический путь произносится, как «число линейно независимых маршрутов через граф от входа к выходу», где:

• «линейно независимый» соответствует однородности и означает, что один не возвращается в исходное состояние двойного счета;
• «маршрут» соответствует нальной однородности: маршруту соответствует одномерный объект;
• «относительно» означает, что путь должен начаться и закончится в точке входа или выхода, соответственно.

Это соответствие интуитивно понятно как цикломатическая вложенность, и может быть вычислено как указанно выше.

Кроме того, его можно вычислить через абсолютное число Бетти определяющее все терминальные узлы данного компонента, в этом случае получаем:

Это соответствие характеризуется цикломатической сложностью как «количество циклов плюс количество компонентов».

Этимология

Название цикломатическая сложность может попервоначалу показаться не являющимся целостным, но это не так, так как эта метрика не только считает циклы в программе. Она должна быть первостепенно заинтересована в подсчёте количества других циклов, тех, которые контролируются по построенному по программе графу, которые заключаются в присутствии веток возврата, которые выявляются при построении графа.