Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Триггер - Триггеры с любым числом устойчивых состояний22 января 2011Оглавление: 1. Триггер 2. История 3. Классификация 4. Базовые понятия 5. RS-триггеры 6. D-триггеры 7. T-триггеры 8. JK-триггеры 9. Триггеры с любым числом устойчивых состояний 10. Триггеры с тиристорами
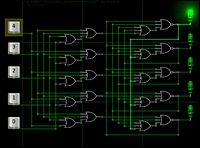
Модель пятеричного RS1S2S3S4-триггера в логическом симуляторе Atanua
Триггер с любым числом устойчивых состояний N строится из N логических элементовИЛИ-НЕ илиИ-НЕ путём соединения выхода каждого элемента) с соответствующими входами всех других элементов. То есть наименьшее число логических элементов для построения N-ичного триггера равно N. Триггеры на элементахИЛИ-НЕ работают в прямом одноединичном коде. Триггеры на элементахИ-НЕ работают в инверсном однонулевом коде. При добавлении N транзисторов доступа эти триггеры могут работать как ячейки статической сверхоперативной памяти. При добавлении схем управления переключением эти триггеры могут работать как N-ичные аналоги двоичного RS-триггера. В непозиционных системах счисления: 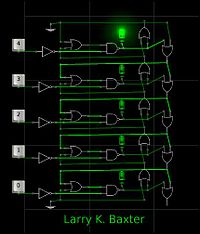
Снимок модели пятеричного RS1S2S3S4-триггера Larry K. Baxter’а в логическом симуляторе Atanua
В приведённом выше подходе построения триггеров с любым числом устойчивых состояний при увеличении числа устойчивых состояний — n, увеличивается число входов в логических элементах в каждой элементарной ячейке триггера. Larry K. Baxter, Lexington, Mass. Assignee: Shintron Company, Inc., Cambridge, Mass. US Patent 3,764,919 Oct. 9, 1973 Filed: Dec. 22, 1972 Fig.3 предлагает другой подход к построению триггеров с любым числом устойчивых состояний, при котором число логических элементов и число входов в логических элементах в каждой элементарной ячейке триггера остаётся постоянным. Просмотров: 29660
|
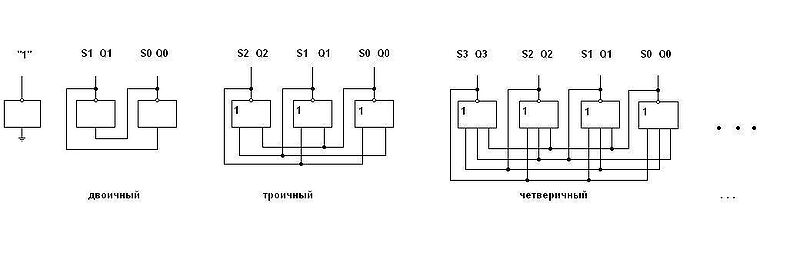
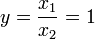 , где x1 — число инверторов, x2 — число состояний триггера.
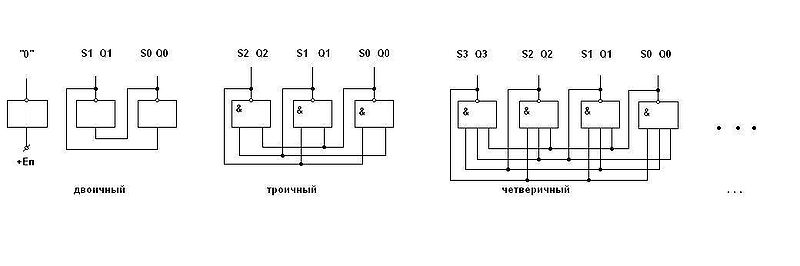
, где x1 — число инверторов, x2 — число состояний триггера.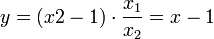 , где x1 — число инверторов, x2 — число состояний триггера, — число диодов в логической части одного логического элемента. По этому параметру выгоднее двоичные триггеры.
, где x1 — число инверторов, x2 — число состояний триггера, — число диодов в логической части одного логического элемента. По этому параметру выгоднее двоичные триггеры.