Интернет магазин китайских планшетных компьютеров |
|||
Компьютеры - Тестирование псевдослучайных последовательностей - Статистические тесты23 января 2011Оглавление: 1. Тестирование псевдослучайных последовательностей 2. Графические тесты 3. Статистические тесты 4. Практические приложения В отличие от графических тестов, статистические тесты выдают численную характеристику последовательности и позволяют однозначно сказать, пройден ли тест. Наиболее известны следующие программные пакеты статистических тестов:
Тесты DIEHARDТесты DIEHARD были разработаны Джорджем Марсальей в течение нескольких лет и впервые опубликованы на CD-ROM, посвящённом случайным числам. Они рассматриваются как один из наиболее строгих известных наборов тестов. Тесты Д. КнутаТесты Кнута основаны на статистическом критерии χ. Вычисляемое значение статистики χ сравнивается с табличными результатами, и в зависимости от вероятности появления такой статистики делается вывод о ее качестве. Среди достоинств этих тестов — небольшое их количество и существование быстрых алгоритмов выполнения. Недостаток — неопределенность в трактовке результатов. Вот краткое описание этих тестов:
Тесты NISTОтличие этих тестов от других современных — открытость алгоритмов. Также среди достоинств — однозначная интерпретация результатов тестирования. Таблица общих характеристик:
Просмотров: 5307
|
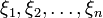 — последовательность длины n и размерности m. Исследуются подпоследовательности определённой длины, содержащие каждое m-разрядное число.
— последовательность длины n и размерности m. Исследуются подпоследовательности определённой длины, содержащие каждое m-разрядное число.