Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Теорема Шеннона об источнике шифрования22 января 2011Оглавление: 1. Теорема Шеннона об источнике шифрования 2. Доказательство теоремы об источнике шифрования 3. Доказательство теоремы об источнике шифрования для кодов символов В теории информатики Теорема Шеннона об источнике шифрования устанавливает предел максимального сжатия данных и числовое значение энтропии Шеннона. Теорема Шеннона об источнике шифрования показывает, что случайных переменных данные стремятся к бесконечности) невозможно сжать данные настолько, что оценка кода меньше чем энтропия Шеннона исходных данных, без потери точности информации. Тем не менее можно получить код, близкий к энтропии Шеннона без значительных потерь. Теорема об источнике шифрования для кодов символов приводит верхнюю и нижнюю границу к минимально возможной длине зашифрованных слов как функция энтропии от входного слова и от размера требуемой азбуки. УтверждениеИсходный код — это отображение из хранилища информации в последовательность алфавитных символов таких что исходный символ может быть однозначно получен из двоичных разрядов или получен с некоторым различием. Это идея сжатия данных. Источник шифрования для кодов символовВ информатике Теорема об источнике шифрования утверждает что:
Теорема об источнике шифрования для кодов символовПусть Σ1, Σ2 значат два конечных алфавита, и пусть Предположим что X — случайная переменная которая принимает значение из Σ1 а f — поддающийся расшифровке код из Если f является оптимальным в смысле что она имеет минимальную длину слова для X, тогда Просмотров: 4184
|
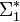 и
и 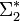 означают набор всех конечных слов из этих алфавитов.
означают набор всех конечных слов из этих алфавитов.