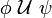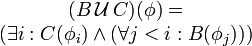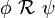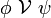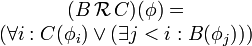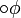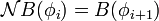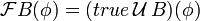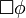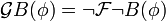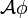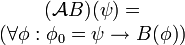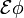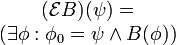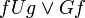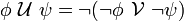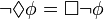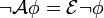Темпоральная логика - Темпоральные операторы

Интернет магазин китайских планшетных компьютеров

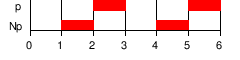
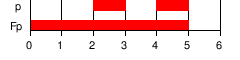
Компьютеры - Темпоральная логика - Темпоральные операторы

23 января 2011

Оглавление:
1. Темпоральная логика
2. Темпоральные операторы
3. Приложения

В темпоральных логиках бывает два вида операторов: логические и модальные. В качестве логических операторов обычно используются. Модальные операторы, используемые в логике линейного времени и логике деревьев вычислений, определяются следующим образом.

Текстовое обозначение	Символьное обозначение	Определение	Описание	Диаграмма
Бинарные операторы
φ U ψ	$\phi ~\mathcal{U}~ \psi$	$\begin{matrix}= \\\land))\end{matrix}$	Until: ψ должно выполниться в некотором состоянии в будущем, свойство φ обязано выполняться во всех состояниях до обозначенного.
φ R ψ φ V ψ	$\phi ~\mathcal{R}~ \psi$ $\phi ~\mathcal{V}~ \psi$	$\begin{matrix}= \\\lor))\end{matrix}$	Release: φ освобождает ψ, если ψ истинно, пока не наступит момент, когда φ первый раз станет истинно. Иначе, φ должно хотя бы раз стать истинным, пока ψ не стало истинным первый раз.
Унарные операторы
N φ X φ	$\circ \phi$	$\mathcal{N}B=B$	NeXt: φ должно быть истинным в состоянии, непосредственно следующим за данным.
F φ	$\Diamond \phi$	$\mathcal{F}B=$	Future: φ должно стать истинным хотя бы в одном состоянии в будущем.
G φ	$\Box \phi$	$\mathcal{G}B=\neg\mathcal{F}\neg B$	Globally: φ должно быть истинно во всех будущих состояниях.
A φ	$\mathcal{A} \phi$	$\begin{matrix}= \\)\end{matrix}$	All: φ должно выполняться на всех ветвях, начинающихся с данной.
E φ	$\mathcal{E} \phi$	$\begin{matrix}= \\)\end{matrix}$	Exists: существует хотя бы одна ветвь, на которой φ выполняется.