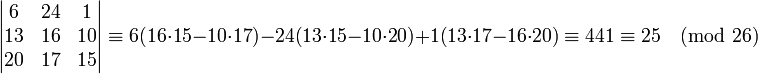Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Шифр Хилла - Расшифрование23 января 2011Оглавление: 1. Шифр Хилла 2. Расшифрование 3. Криптостойкость 4. Механическая реализация Для того, чтобы расшифровать сообщение, необходимо обратить шифротекст обратно в вектор и затем просто умножить на обратную матрицу ключа. В Возьмем шифротекст из предыдущего примера 'WLY'. Тогда мы получим что возвращает нас к сообщению 'DOG', как мы и рассчитывали. Необходимо обсудить некоторые сложности, связанные с выбором шифрующей матрицы. Не все матрицы имеют обратную. Матрица будет иметь обратную в том и только в том случае, когда ее детерминант не равен нулю и не имеет общих делителей с основанием модуля. Таким образом, если мы работаем с основанием модуля 26 как в примерах выше, то детерминант должен быть ненулевым и не делиться на 2 и 13. Если детерминант матрицы равен нулю или имеет общие делители с основанием модуля, то такая матрица не может использоваться в шифре Хилла, и должна быть выбрана другая матрица. Тем не менее, матрицы, которые удовлетворяют вышеприведенным условиям, существуют в изобилии. Детерминант матрицы из примера: Итак, детерминант равен 25 по модулю 26. Так число 25 не имеет общих делителей с числом 26, то матрица с таким детерминантом может использоваться в шифре Хилла. Опасность того, что детерминант матрицы ключа будет иметь общие делители с основанием модуля может быть устранена путем выбирания простого числа в качестве основания модуля. Например, в более удобном варианте шифра Хилла в алфавит добавляют 3 дополнительных символа, чтобы увеличить основание модуля до 29. Просмотров: 6326
|
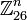 обратная матрица к использованной в примере шифрования будет
обратная матрица к использованной в примере шифрования будет