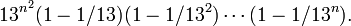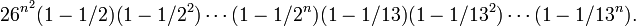Интернет магазин китайских планшетных компьютеров

Компьютеры - Шифр Хилла - Криптостойкость

К сожалению, стандартный шифр Хилла уязвим к атаке по выбранному открытому тексту, потому что он полностью линейный. Криптоаналитик, который перехватит n пар символ сообщения/символ шифротекста сможет составить систему линейных уравнений, которую обычно не сложно решить. Если окажется, что система не решаема,то необходимо всего лишь добавить еще несколько пар символ сообщения/символ шифротекста. Такого рода расчеты средствами обычных алгоритмов линейной алгебры требует совсем немного времени.

Длина ключа

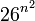Длина ключа — это двоичный логарифм от количества всех возможных ключей. Существует матриц размера n × n. Значит, 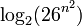или приблизительно 4.7n — верхняя грань длины ключа для шифра Хилла, использующего матрицы n × n. Это только верхняя грань, поскольку не каждая матрица обратима, а только такие матрицы могут быть ключом. Количество обратимых матриц может быть рассчитано при помощи Китайской теоремы об остатках. Т. е. матрица обратима по модулю 26 тогда и только тогда, когда она обратима и по модулю 2 и по модулю 13. Количество обратимых по модулю 2 матриц размера n × n равно порядку линейной группы GL. Это

Аналогично, количество обратимых по модулю 13 матриц) равно

Количество обратимых по модулю 26 матриц равно произведению этих двух чисел. Значит,

Кроме того будет разумно избегать слишком большого количества нулей в матрице-ключе, так как они уменьшают диффузию. В итоге получается, что эффективное пространство ключей стандартного шифра Хилла составляет около 4.64n − 1.7. Для шифра Хилла 5 × 5 это составит приблизительно 114 бит. Очевидно, полный перебор — не самая эффективная атака на шифр Хилла.