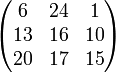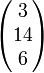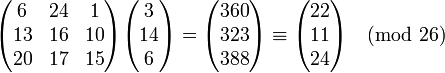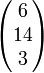Интернет магазин китайских планшетных компьютеров |
|||||||||||||||||||||||||
Компьютеры - Шифр Хилла23 января 2011Оглавление: 1. Шифр Хилла 2. Расшифрование 3. Криптостойкость 4. Механическая реализация Шифр Хилла — полиграммный шифр подстановки, основанный на линейной алгебре. Лестер С. Хилл изобрел этот шифр в 1929, и это был первый шифр, который позволял на практике оперировать более чем с тремя символами за раз. Последующее обсуждение шифра предполагает начальные знания матриц. ШифрованиеКаждой букве сперва сопоставляется число. Для латинского алфавита часто используется простейшая схема: A = 0, B =1, ..., Z=25, но это не является существенным свойством шифра. Блок из n букв рассматривается как n-мерный вектор и умножается на n × n матрицу по модулю 26. Матрица целиком является ключом шифра. Матрица должна быть обратима в В следующих примерах используются латинские буквы от A до Z, соответствующие им численные значения приведены в таблице.
Рассмотрим сообщение 'DOG' и представленный ниже ключ: Так как букве 'D' соответствует число 3, 'O' — 14, 'G' — 6, то сообщение — это вектор Тогда зашифрованный вектор будет что соответствует шифротексту 'WLY'. Теперь предположим, что наше сообщение было 'GOD' или Теперь зашифрованный вектор будет что соответствует шифротексту 'LUN'. Видно, что каждая буква шифротекста сменилась. Шифр Хилла достиг диффузии по Шеннону, и n-размерный шифр Хилла может достигать диффузии n символов за раз. Просмотров: 6319
|
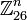, чтобы была возможна операция расшифрования.
