Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Схема разделения секрета Шамира - Описание23 января 2011Оглавление: 1. Схема разделения секрета Шамира 2. Описание 3. Пример Пусть нужно разделить секрет M между n сторонами таким образом, чтобы любые k участников могли бы восстановить секрет-пороговую схему). Выберем некоторое простое число p > M. Это число можно открыто сказать всем участникам. Оно задаёт конечное поле размера p. Над этим полем построим многочлен степени k − 1: В этом многочлене M — это разделяемый секрет, а остальные коэффициенты Теперь вычисляем координаты различных n точек: Аргументы не обязательно должны идти по порядку, главное - чтобы все они были различны по модулю p. После этого секреты раздаются сторонам. Случайные коэффициенты Теперь любые k участников, зная координаты k различных точек многочлена, смогут восстановить многочлен и все его коэффициенты, включая последний из них — разделённый секрет. Особенностью схемы является то, что даже k − 1 сторон, собравшихся вместе, не смогут найти секрет даже методом полного перебора всех возможных вариантов. Прямолинейное восстановление коэффициентов многочлена через решение системы уравнений можно заменить на вычисление интерполяционного многочлена Лагранжа. Формула многочлена будет выглядеть следующим образом: где Просмотров: 4019
|
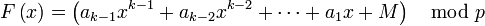
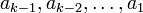 — некоторые случайные числа, которые нужно будет «забыть» после того, как процедура разделения секрета будет завершена.
— некоторые случайные числа, которые нужно будет «забыть» после того, как процедура разделения секрета будет завершена.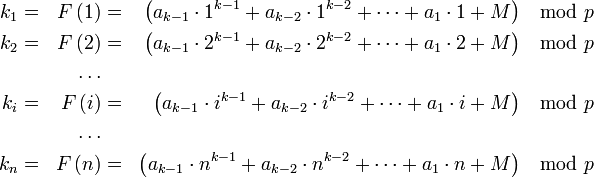
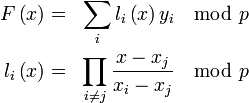
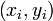 — координаты точек многочлена. Все операции выполняются также в конечном поле p.
— координаты точек многочлена. Все операции выполняются также в конечном поле p.