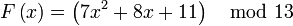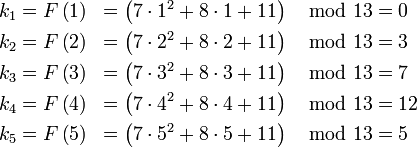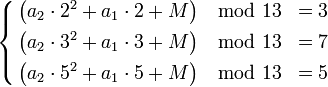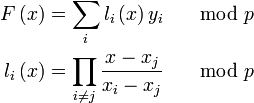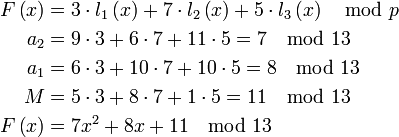Схема интерполяционных полиномов Лагранжа

Интернет магазин китайских планшетных компьютеров

Компьютеры - Схема интерполяционных полиномов Лагранжа - Пример

23 января 2011

Оглавление:
1. Схема интерполяционных полиномов Лагранжа
2. Описание
3. Пример

Пусть нужно разделить секрет «11» между 5-ю сторонами. При этом любые 3 стороны должны иметь возможность восстановить этот секрет. То есть нужно реализовать -пороговую схему.

Возьмём простое число p = 13. Построим многочлен степени k − 1 = 3 − 1 = 2:

$F \left = \left \mod 13$

В этом многочлене 11 — это разделяемый секрет, а остальные коэффициенты 7 и 8 — некоторые случайные числа, которые нужно будет «забыть» после того, как процедура разделения секрета будет завершена.

Теперь вычисляем координаты 5 различных точек:

$\begin{align} k_1 &= F \left &= \left \mod 13 &= 0 \\ k_2 &= F \left &= \left \mod 13 &= 3 \\ k_3 &= F \left &= \left \mod 13 &= 7 \\ k_4 &= F \left &= \left \mod 13 &= 12 \\ k_5 &= F \left &= \left \mod 13 &= 5 \\ \end{align}$

После этого секреты раздаются сторонам. Случайные коэффициенты 7,8 и сам секрет M = 11 «забываются».

Теперь любые 3 участника смогут восстановить многочлен и все его коэффициенты, включая последний из них — разделённый секрет. Например, чтобы восстановить многочлен по трём долям k₂,k₃,k₅ им нужно будет решить систему:

$\left\{\begin{align} \left &\mod 13 &= 3 \\ \left &\mod 13 &= 7 \\ \left &\mod 13 &= 5 \\ \end{align} \right.$

Очевидно, что с меньшим числом известных секретов получится меньше уравнений и систему решить будет нельзя.

Построим интерполяционный многочлен Лагранжа:

$\begin{align} F\left &= \sum\limits_i {l_i \lefty_i } &\mod p \\ l_i \left &= \prod\limits_{i \ne j} {\frac{{x - x_j }}{{x_i - x_j }}} &\mod p \\ \end{align}$

$\begin{align} l_1 \left &= \frac{{x - x_2 }}{{x_1 - x_2 }} \cdot \frac{{x - x_3 }}{{x_1 - x_3 }} = \frac{{x - 3}}{{2 - 3}} \cdot \frac{{x - 5}}{{2 - 5}} = \frac{1}{3}\left = 9\left = 9x^2 + 6x + 5 \mod 13 \\ l_2 \left &= \frac{{x - x_1 }}{{x_2 - x_1 }} \cdot \frac{{x - x_3 }}{{x_2 - x_3 }} = \frac{{x - 2}}{{3 - 2}} \cdot \frac{{x - 5}}{{3 - 5}} = \frac{1}{{11}}\left = 6\left = 6x^2 + 10x + 8 \mod 13 \\ l_3 \left &= \frac{{x - x_1 }}{{x_3 - x_1 }} \cdot \frac{{x - x_2 }}{{x_3 - x_2 }} = \frac{{x - 2}}{{5 - 2}} \cdot \frac{{x - 3}}{{5 - 3}} = \frac{1}{6}\left = 11\left = 11x^2 + 10x + 1 \mod 13 \end{align}$

$\begin{align} F\left &= 3 \cdot l_1 \left + 7 \cdot l_2 \left + 5 \cdot l_3 \left \mod p \\ a_2 &= 9 \cdot 3 + 6 \cdot 7 + 11 \cdot 5 = 7 \mod 13 \\ a_1 &= 6 \cdot 3 + 10 \cdot 7 + 10 \cdot 5 = 8 \mod 13 \\ M &= 5 \cdot 3 + 8 \cdot 7 + 1 \cdot 5 = 11 \mod 13 \\ F\left &= 7 x ^ 2 + 8 x + 11 \mod 13 \end{align}$

Последний коэффициент многочлена — M = 11 — и является секретом.

<<< Схема Блэкли

Компьютерное аппаратное обеспечение
Вычислительные комплексы
Компьютерные данные
Компьютерные журналы
Классы компьютеров
Компьютеры

Программное обеспечение
Производители компьютеров
Профессии в ИТ
Системное администрирование
Компьютерный сленг
Списки компьютерных терминов

Человеко-компьютерное взаимодействие