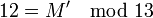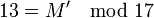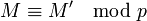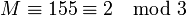Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Схема Асмута Блума23 января 2011Схема Асмута — Блума — пороговая схема разделения секрета, построенная с использованием простых чисел. Позволяет разделить секрет между n сторонами таким образом, что его смогут восстановить любые m участников. ОписаниеПусть M - некоторый секрет, который требуется разделить. Выбирается простое число p, большее M. Выбирается n взаимно простых друг с другом чисел Выбирается случайное число r и вычисляется
Вычисляются доли: Участникам раздаются Теперь, используя китайскую теорему об остатках можно восстановить секрет M имея m и более долей. ПримерПредположим нам нужно разделить секрет M = 2 между 4-мя участниками таким образом, чтобы любые 3 из них могли этот секрет восстановить. То есть нужно реализовать-пороговую схему. В качестве простого числа выберем p = 3, в качестве взаимно простых - 11,13,17,19. Проверяем, что:
Выбираем случайное число r = 51 и вычисляем:
Вычисляем доли: Теперь попробуем восстановить исходный секрет, имея на руках доли Мы можем восстановить M', используя китайскую теорему об остатках. Зная M' мы восстанавливаем секрет. Просмотров: 2326
|
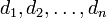 , таких что:
, таких что: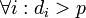
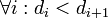
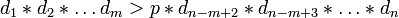
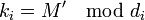
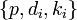
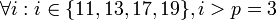
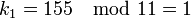
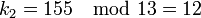
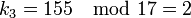
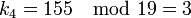
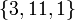 ,
, 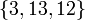 ,
, 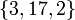 . Составим систему уравнений:
. Составим систему уравнений: