|
|
|
Компьютеры - Самоорганизующаяся карта Кохонена - Работа сети23 января 2011
Оглавление:
1. Самоорганизующаяся карта Кохонена
2. Работа сети
3. История
- Инициализация карты, то есть первоначальное задание векторов веса для узлов.
- Цикл:
- Выбор следующего наблюдения.
- Нахождение для него лучшей единицы соответствия — узла на карте, вектор веса которого меньше всего отличается от наблюдения.
- Определение количества соседей BMU и обучение — изменение векторов веса BMU и его соседей с целью их приближения к наблюдению.
- Определение ошибки карты.
Алгоритм
Наиболее распространены три способа задания первоначальных весов узлов:
-
- Задание всех координат случайными числами.
- Присваивание вектору веса значение случайного наблюдения из входных данных.
- Выбор векторов веса из линейного пространства, натянутого на главные компоненты набора входных данных.
Пусть t — номер итерации.
-
- Выбрать произвольное наблюдение x из множества входных данных.
- Найти расстояния от него до векторов веса всех узлов карты и определить ближайший по весу узел Mc. Это — BMU или Winner. Условие на Mc:
 , ,- для любого mi, где mi — вектор веса узла Mi. Если находится несколько узлов, удовлетворяющих условию, BMU выбирается случайным образом среди них.
-
- Определить с помощью функции h соседей Mc и изменение их векторов веса.
-
- Функция определяет "меру соседства" узлов Mi и Mc и изменение векторов веса. Она должна постепенно уточнять их значения, сначала у большего количества узлов и сильнее, потом у меньшего и слабее. Часто в качестве функции соседства используется гауссовская функция:
-
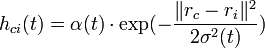
-
- где 0 < α < 1 — обучающий сомножитель, монотонно убывающий с каждой последующей итерацией;
- ri, rc — координаты узлов Mi и Mc на карте;
- σ — сомножитель, уменьшающий количество соседей с итерациями, монотонно убывает.
- Параметры α, σ и их характер убывания задаются аналитиком.
-
- Более простой способ задания функции соседства:
-
- hci = α,
-
- если Mi находится в окрестности Mc заранее заданного аналитиком радиуса, и 0 в противном случае.
-
- Функция h равна α для BMU и уменьшается с удалением от BMU.
-
- Изменить вектор веса по формуле:
-
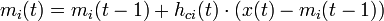
-
- Т.о. вектора веса всех узлов, являющихся соседями BMU, приближаются к рассматриваемому наблюдению.
- Например, как среднее арифметическое расстояний между наблюдениями и векторами веса соответствующих им BMU:
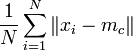 , ,
- где N - количество элементов набора входных данных.
Просмотров: 3025
|
 ,
,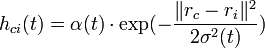
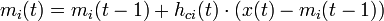
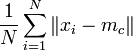 ,
,