|
|
|
Компьютеры - RSA - Описание алгоритма29 мая 2011
Оглавление:
1. RSA
2. Описание алгоритма
Введение
Криптографические системы с открытым ключом используют так называемые необратимые функции, которые обладают следующим свойством:
- Если известно
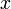 , то , то 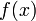 вычислить относительно просто вычислить относительно просто
- Если известно
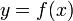 , то для вычисления , то для вычисления 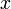 нет простого пути. нет простого пути.
Под однонаправленностью понимается не теоретическая однонаправленость, а практическая невозможность вычислить обратное значение, используя современные вычислительные средства, за обозримый интервал времени.
В основу криптографической системы с открытым ключом RSA положена задача умножения и разложения составных чисел на простые сомножители, которая является вычислительно однонаправленной задачей .
В криптографической системе с открытым ключом каждый участник располагает как открытым ключом, так и закрытым ключом. Каждый ключ — это часть информации. В криптографической системе RSA каждый ключ состоит из пары целых чисел. Каждый участник создаёт свой открытый и закрытый ключ самостоятельно. Закрытый ключ каждый из них держит в секрете, а открытые ключи можно сообщать кому угодно или даже публиковать их. Открытый и закрытый ключи каждого участника обмена сообщениями образуют «согласованную пару» в том смысле, что они являются взаимно обратными, т.е
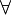 сообщения сообщения 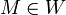 , где , где 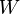 — множество допустимых сообщений. — множество допустимых сообщений.
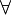 открытого и секретного ключа открытого и секретного ключа 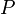 и и 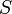
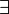 соответствующие функции шифрования соответствующие функции шифрования 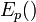 и расшифрования и расшифрования 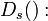
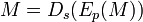
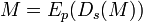
Алгоритм создания открытого и секретного ключей
RSA-ключи генерируются следующим образом:
- Выбираются два случайных простых числа p и q заданного размера.
- Вычисляется их произведение n = pq, которое называется модулем.
- Вычисляется значение функции Эйлера от числа n:
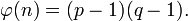
- Выбирается целое число e" src="http://upload.wikimedia.org/math/5/b/8/5b8e85fcd4e4122799d95918630b0264.png" />), взаимно простое со значением функции
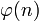 . Обычно в качестве e берут простые числа, содержащие небольшое количество единичных битов в двоичной записи, например, простые числа Ферма 17, 257 или 65537. . Обычно в качестве e берут простые числа, содержащие небольшое количество единичных битов в двоичной записи, например, простые числа Ферма 17, 257 или 65537.
- Число e называется открытой экспонентой
- Время, необходимое для шифрования с использованием быстрого возведения в степень, пропорционально числу единичных бит в e.
- Слишком малые значения e, например 3, потенциально могут ослабить безопасность схемы RSA.
- Вычисляется число d, мультипликативно обратное к числу e по модулю
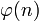 , то есть число, удовлетворяющее условию: , то есть число, удовлетворяющее условию:
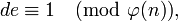 или: или: 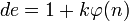 , где k — некоторое целое число. , где k — некоторое целое число.
- Примечание: Можно вычислять и так mod*) = 1. Результат операции i mod j — остаток от целочисленного деления i на j, то есть если имеем mod 20 = 1. Значит d будет, например 7..
- Число d называется секретной экспонентой.
- Обычно, оно вычисляется при помощи расширенного алгоритма Евклида.
- Пара P = публикуется в качестве открытого ключа RSA.
- Пара S = играет роль секретного ключа RSA и держится в секрете.
Шифрование и расшифрование
Схема RSA
Предположим, сторона 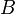 хочет послать стороне хочет послать стороне 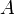 сообщение сообщение 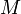 . .
Сообщением являются целые числа лежащие от 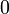 до до 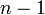 , т.е , т.е 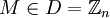 . .
Корректность схемы RSA
- Уравнения
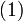 и и 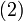 , на которых основана схема RSA, определяют взаимно обратные преобразования множества , на которых основана схема RSA, определяют взаимно обратные преобразования множества 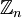
Просмотров: 3597
|

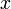 , то
, то 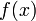 вычислить относительно просто
вычислить относительно просто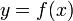 , то для вычисления
, то для вычисления 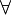 сообщения
сообщения 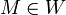 , где
, где 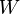 — множество допустимых сообщений.
— множество допустимых сообщений.
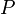 и
и 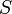
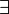 соответствующие функции шифрования
соответствующие функции шифрования 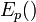 и расшифрования
и расшифрования 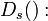
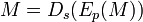
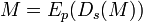
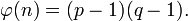
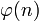 . Обычно в качестве e берут простые числа, содержащие небольшое количество единичных битов в двоичной записи, например, простые числа Ферма 17, 257 или 65537.
. Обычно в качестве e берут простые числа, содержащие небольшое количество единичных битов в двоичной записи, например, простые числа Ферма 17, 257 или 65537.
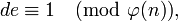 или:
или: 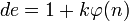 , где k — некоторое целое число.
, где k — некоторое целое число.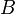 хочет послать стороне
хочет послать стороне 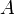 сообщение
сообщение 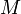 .
.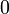 до
до 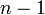 , т.е
, т.е 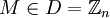 .
.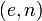 стороны
стороны 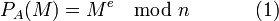
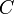
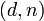 для расшифровки сообщения:
для расшифровки сообщения: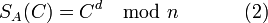
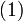 и
и 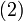 , на которых основана схема RSA, определяют взаимно обратные преобразования множества
, на которых основана схема RSA, определяют взаимно обратные преобразования множества