Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Решето Эратосфена - Псевдокод23 января 2011Оглавление: 1. Решето Эратосфена 2. Псевдокод 3. Решето Эйлера
Вход: натуральное число n
Пусть A — булевый массив, индексируемый числами от 2 до n,
изначально заполненный значением true.
count = n - 1
для i = 2, 3, 4, ..., пока i^2 ≤ n:
если A = true:
для j = i^2, i^2 + i, i^2 + 2i, ..., пока j ≤ n:
если A = true:
A = false
count = count - 1
Теперь все числа i, такие что A = true, являются простыми,
а переменная count содержит в себе их общее количество в массиве.
Пример для n = 30Запишем натуральные числа начиная от 2 до 30 в ряд: 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 Первое число в списке, 2 — простое. Пройдём по ряду чисел, вычёркивая все числа кратные 2: 2 3 Следующее невычеркнутое число, 3 — простое. Пройдём по ряду чисел, вычёркивая все числа кратные 3: 2 3 Следующее невычеркнутое число, 5 — простое. Пройдём по ряду чисел, вычёркивая все числа кратные 5. И т. д. 2 3 Необходимо провести вычёркивания кратных для всех простых чисел p, для которых 2 3 5 7 11 13 17 19 23 29 Просмотров: 6520
|
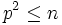. В результате все составные числа будут вычеркнуты, а невычеркнутыми останутся все простые числа. Для n = 30 уже после вычёркивания кратных числу 5 все составные числа получаются вычеркнутыми: