|
|
|
Компьютеры - Решето Аткина - Объяснение23 января 2011
Оглавление:
1. Решето Аткина
2. Объяснение
3. Оценка сложности
- Все числа, равные 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, или 58, делятся на два и заведомо не простые. Все числа, равные 3, 9, 15, 21, 27, 33, 39, 45, 51, или 57, делятся на три и тоже не являются простыми. Все числа, равные 5, 25, 35, или 55, делятся на пять и также не простые. Все эти остатки игнорируются.
- Все числа, равные 1, 13, 17, 29, 37, 41, 49 или 53, имеют остаток от деления на 4 равный 1. Эти числа являются простыми тогда и только тогда, когда количество решений уравнения 4x² + y² = n нечётно и само число не кратно никакому квадрату простого числа.
- Числа, равные 7, 19, 31, или 43, имеют остаток от деления на 6 равный 1. Эти числа являются простыми тогда и только тогда, когда количество решений уравнения 3x² + y² = n нечётно и само число не кратно никакому квадрату простого.
- Числа, равные 11, 23, 47, или 59, имеют остаток от деления на 12 равный 11. Эти числа являются простыми тогда и только тогда, когда количество решений уравнения 3x² − y² = n нечётно и само число не кратно никакому квадрату простого.
Ни одно из рассматриваемых чисел не делится на 2, 3, или 5, соответственно, они не могут делиться и на их квадраты. Поэтому проверка, что число не кратно квадрату простого числа, не включает 2², 3², и 5².
Особенности полной версии алгоритма
Сегментация
Для уменьшения требований к памяти «просеивание» производится порциями, размер которых составляет примерно 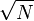 . .
Предпросеивание
Для ускорения работы полная версия алгоритма игнорирует все числа, которые кратны одному из нескольких первых простых чисел. Это делается путем использования стандартных структур данных и алгоритмов их обработки, предложенных ранее Полом Притчардом. Они известны под названием англ. wheel sieving. Количество первых простых чисел выбирается в зависимости от заданного числа N. Теоретически предлагается брать первые простые примерно до 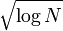 . Это позволяет улучшить асимптотическую оценку скорости алгоритма на множитель . Это позволяет улучшить асимптотическую оценку скорости алгоритма на множитель 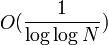 . При этом требуется дополнительная память, которая с ростом N ограничена как . При этом требуется дополнительная память, которая с ростом N ограничена как 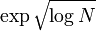 . Увеличение требований к памяти оценивается как . Увеличение требований к памяти оценивается как 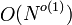 . .
Версия, представленная на сайте авторов, оптимизирована для поиска всех простых чисел до миллиарда, в ней исключаются из вычислений числа кратные двум, трём, пяти и семи.
Просмотров: 5423
|
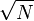 .
.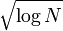 . Это позволяет улучшить асимптотическую оценку скорости алгоритма на множитель
. Это позволяет улучшить асимптотическую оценку скорости алгоритма на множитель 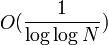 . При этом требуется дополнительная память, которая с ростом N ограничена как
. При этом требуется дополнительная память, которая с ростом N ограничена как 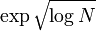 . Увеличение требований к памяти оценивается как
. Увеличение требований к памяти оценивается как 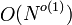 .
.