|
|
|
Компьютеры - Регистр сдвига с линейной обратной связью - Свойства22 января 2011
Оглавление:
1. Регистр сдвига с линейной обратной связью
2. Свойства
3. Пример
4. Преимущества
Свойства выдаваемой РСЛОС последовательности тесно связаны со свойствами ассоциированного многочлена 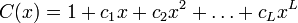 над полем над полем 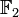 . Его ненулевые коэффициенты называются отводами, как и соответствующие ячейки регистра, поставляющие значения аргументов функции обратной связи. . Его ненулевые коэффициенты называются отводами, как и соответствующие ячейки регистра, поставляющие значения аргументов функции обратной связи.
Периодичность
Так как существует 2 − 1 разных ненулевых состояний регистра, то период последовательности, генерируемой РСЛОС при любом ненулевом начальном состоянии, не превышает 2 − 1. При этом период зависит от ассоциированного многочлена:
- если старший коэффициент ассоциированного многочлена CL равен нулю, то периодичная часть генерируемой последовательности может проявляться не сразу;
- если CL = 1, то соответствующая последовательность называется неособой. Такая последовательность начинается со своей периодичной части. Наиболее интересны неособые последовательности, соответствующие многочленам со следующими дополнительными свойствами:
- если C неприводим, то при любом ненулевом начальном состоянии регистра период генерируемой последовательности равен наименьшему числу N, при котором многочлен C делит 1 + x. Как следствие, период последовательности будет делить число 2 − 1;
- если C примитивен, то любое ненулевое начальное состояние регистра дает последовательность с максимально возможным периодом 2 − 1. Например, РСЛОС с отводной последовательностью, состоящей из первого и четвёртого битов имеет максимальный период тогда и только тогда, когда ассоциированный многочлен x + x + 1 является примитивным.
Линейная сложность
Линейная сложность бинарной последовательности — одна из самых важных характеристик работы РСЛОС. Введём следующие обозначения:
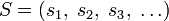 — бесконечная последовательность; — бесконечная последовательность;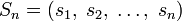 — подпоследовательность длины n последовательности S; — подпоследовательность длины n последовательности S;- говорят, что РСЛОС генерирует последовательность S, если существует некоторое исходное состояние, при котором выходная последовательность РСЛОС совпадает S;
- говорят, что РСЛОС генерирует конечную последовательность Sn, если существует некоторое начальное состояние, для которого выходная последовательность РСЛОС имеет в качестве первых n членов члены последовательности Sn.
- Определение
Линейной сложностью бесконечной двоичной последовательности S называется число L, которое определяется следующим образом:
- если
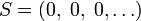 — нулевая последовательность, то L = 0; — нулевая последовательность, то L = 0;
- если не существует РСЛОС, который генерирует S, то
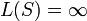 ; ;
- иначе L равна длине самого короткого РСЛОС, который генерирует S.
Линейной сложностью конечной двоичной последовательности Sn называется число L, которое равно длине самого короткого РСЛОС, который генерирует последовательность, имеющую в качестве первых n членов L.
- Свойства линейной сложности
Пусть S и K — двоичные последовательности. Тогда:
- для любого n > 0 линейная сложность подпоследовательности L удовлетворяет неравенствам
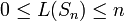 ; ;
- L = 0 тогда и только тогда, когда Sn — нулевая последовательность длины n;
- L = n тогда и только тогда, когда
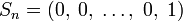 ; ;
- если S периодическая с периодом T, то
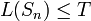 ; ;
 . .
Просмотров: 6432
|
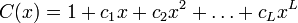 над полем
над полем 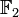 . Его ненулевые коэффициенты называются отводами, как и соответствующие ячейки регистра, поставляющие значения аргументов функции обратной связи.
. Его ненулевые коэффициенты называются отводами, как и соответствующие ячейки регистра, поставляющие значения аргументов функции обратной связи.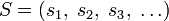 — бесконечная последовательность;
— бесконечная последовательность;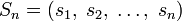 — подпоследовательность длины n последовательности S;
— подпоследовательность длины n последовательности S;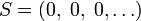 — нулевая последовательность, то L = 0;
— нулевая последовательность, то L = 0;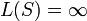 ;
;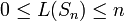 ;
;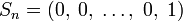 ;
;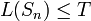 ;
; .
.