Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Ранцевая криптосистема Меркля-Хеллмана - Математическое описание алгоритма23 января 2011Оглавление: 1. Ранцевая криптосистема Меркля-Хеллмана 2. Математическое описание алгоритма 3. Пример Генерация ключаЧтобы зашифровать n-битное сообщение, выберем супервозрастающую последовательность из n ненулевых натуральных чисел
Далее случайным образом выберем целые взаимно простые числа q и r такие, что
Число q выбирается таким образом, чтобы гарантировать единственность шифротекста. В случае, если оно будет хотя бы чуть меньше, может возникнуть ситуация, что одному шифротексту будут соответствовать несколько исходных текстов. r должно быть взаимно просто с q, в противном случае оно не будет иметь мультипликативного обратного по модулю q, существование которого необходимо для расшифровки. Теперь построим последовательность
где каждый элемент вычисляется по следующей формуле
β будет открытым ключом, в то время как закрытый ключ образует последовательность. ШифрованиеЧтобы зашифровать n-битное сообщение
где αi - это i-ый бит, т.е. РасшифровкаЧтобы прочитать исходный текст, получатель должен определить биты сообщения αi, которые удовлетворяли бы формуле Такая задача имела бы полиномиальную сложность в случае, если бы βi были случайно выбранными значениями. Однако значения βi были выбраны таким образом, что расшифровка сводится к простой задаче при условии, что открытый ключ известен. Ключ к определению исходного текста заключается в том, чтобы найти целое число s, которое является мультипликативным обратным r по модулю q. Это значит, что s удовлетворяет уравнению sr mod q = 1, что эквивалентно существованию целого числа k такого, что sr = kq + 1. Поскольку r взаимно просто с q, найти s и k возможно с использованием расширенного алгоритма Евклида. Далее получатель шифротекста вычисляет Отсюда Из того, что rs mod q = 1 и βi= rwi mod q, следует Тогда Сумма всех wi меньше, чем q. Отсюда значение
А это уже простая задача, поскольку w - супервозрастающая последовательность. Пусть wk – наибольший элемент в w. Если wk > c' , то αk = 0; если wk ≤c' , то αk = 1. Далее вычитаем произведение wk×αk из c' и повторяем эти шаги до тех пор, пока не вычислим α. Просмотров: 4947
|
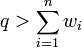 .
.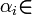 {0, 1}, вычислим число c, которое и будет шифротекстом.
{0, 1}, вычислим число c, которое и будет шифротекстом.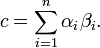
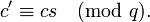
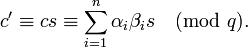
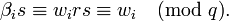
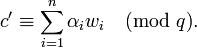
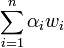 также находится в интервале. Таким образом, получатель должен определить αi из условия, что
также находится в интервале. Таким образом, получатель должен определить αi из условия, что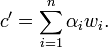 .
.