Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Ранцевая криптосистема Меркля-Хеллмана23 января 2011Преимущества ПАНОРАМНЫЙ ОФТАЛЬМОСКОП PANOPTIC 11820-CE очевидны. Оглавление: 1. Ранцевая криптосистема Меркля-Хеллмана 2. Математическое описание алгоритма 3. Пример Ранцевая криптосистема Меркля-Хеллмана, основанная на «задаче о рюкзаке», была разработана Ральфом Мерклем и Мартином Хеллманом в 1978 году. Это была одна из первых криптосистем с открытым ключом, но она оказалась криптографически нестойкой и, как следствие, не приобрела популярности. Описание«Задача о рюкзаке» заключается в следующем: зная подмножество грузов, уложенных в ранец, легко подсчитать суммарный вес, но, зная вес, непросто определить подмножество грузов. Более подробно, пусть задана последовательность из n положительных чисел
Задача состоит в том, чтобы найти такой бинарный вектор
чтобы
Если каждому двоичному числу x поставить в соответствие некоторую букву алфавита, то её можно было бы передавать в зашифрованном виде просто как сумму s. Для произвольного набора чисел wi задача восстановления x по s является NP-трудной. Р.Мерклю удалось получить обратную к числу s функцию, которая давала бы вектор x, зная только некий «секретный» ключ, и он предложил $100 тому, кто сможет раскрыть ранцевую систему Меркля-Хеллмана. Рассмотрим её подробнее. Меркль использовал не произвольную последовательность wi, а супервозрастающую, то есть такую, что
Нетрудно убедиться, что для такого набора чисел решение задачи является тривиальным. Чтобы избавиться от этой тривиальности и понадобилось ввести «секретный ключ», а именно два числа: q такое, что В итоге получаем: открытый ключ –, закрытый ключ -.
– сообщение x = - вычисляем y = b1x1 + b2x2 + bnx
- вычисляем s = y'r mod q - решаем задачу для s для супервозрастающей последовательности , т.е. находим двоичное число x Награда досталась А. Шамиру после публикации им в марте 1982 года сообщения о раскрытии ранцевой системы Меркля-Хеллмана с одной итерацией. Заметим, что Шамир сумел построить ключ, не обязательно равный секретному, но позволяющий раскрыть шифр. Итак, это была одна из неудачных, но очень интересных попыток построения криптосистемы на основе задачи о рюкзаке. Генерация ключаВ системе Меркля-Хеллмана ключи состоят из последовательностей. Открытый ключ представляет собой «сложную» последовательность, закрытый ключ состоит из «простой» или супервозрастающей последовательности, а также двух дополнительных чисел – множителя и модуля, которые используются как для преобразования супервозрастающей последовательности в «сложную», так и для преобразования суммы подмножества «сложной» последовательности в сумму подмножества «простой». Последняя задача решается за полиномиальное время. ШифрованиеСначала исходный текст необходимо представить в двоичном виде и разбить его на блоки, равные по длине с открытым ключом. Далее из последовательности, образующей открытый ключ, выбираются только те элементы, которые по порядку соответствуют 1 в двоичной записи исходного текста, игнорируя при этом элементы, соответствующие 0 биту. После этого элементы полученного подмножества складываются. Найденная в результате сумма и есть шифротекст. РасшифровкаРасшифровка является возможной в силу того, что множитель и модуль, используемые для генерации открытого ключа из супервозрастающей последовательности, используются также и для преобразования шифротекста в сумму соответствующих элементов супервозрастающей последовательности. Далее, с помощью простого жадного алгоритма, можно расшифровать сообщение, используя O арифметических операций. Просмотров: 4916
|
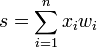 .
.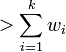 .
.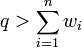 и r такое, что НОД =1. И теперь вместо первоначального набора чисел wi будем использовать числа bi=rwi mod q. В оригинальных статьях Меркль рекомендовал использовать n порядка 100, где n - число элементов супервозрастающей последовательности.
и r такое, что НОД =1. И теперь вместо первоначального набора чисел wi будем использовать числа bi=rwi mod q. В оригинальных статьях Меркль рекомендовал использовать n порядка 100, где n - число элементов супервозрастающей последовательности.