Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Q-метод Полларда дискретного логарифмирования22 января 2011алгоритм дискретного логарифмирования в кольце вычетов по простому модулю, имеющий экспоненциальную сложность. Он был предложен Поллардом в 1978 году. Основные идеи алгоритма очень похожи на идеи ρ-метода Полларда факторизации. Постановка задачиДля заданного простого числа p и двух целых чисел a и b требуется найти целое число x, удовлетворяющее сравнению:
Идея алгоритмаРассматриваются три числовые последовательности:
определённые следующим образом:
Замечание: везде рассматривается наименьшие неотрицательные вычеты. Далее рассматриваются наборы
Если при этом
Компьютерная реализацияМодифицированный интерфейс modЭто делать не нужно, но многие формулы после этого выглядят более естественно
def mod:
'''
Ввел для удобства использования
в функции solve,
так очевиднее, что куда передается нежели c %
'''
return a % b
Расширенный алгоритм Евклида
## ExtendedGCD
# *********************************************************
def ExtendedGCD:
'''
Из книги Т. Корман <<Алгоритмы. Построение и Анализ>>
стр 966
'''
if b == 0:
return a , 1, 0
d1, x1, y1 = ExtendedGCD )
d, x, y = d1, y1, x1 - *y1
return d, x, y
Функция Эйлера
## EulerPhi
# *********************************************************
def EulerPhi:
'''
Функция Эйлера
varphi, где n — натуральное число,
равна количеству натуральных чисел,
не больших n и взаимно простых с ним.
'''
res = 1
i = 2
while:
# пока i^2 <= input
p = 1
while:
input /= i # если не взаимно просты, делим
p *= i # произведение делителей i втч и кратных
p /= i
if :
# если мы хоть раз делили на текущее i
# то общее произведение делителей
# уиножаем на*i^
res *= )
i += 1
n = input - 1
# input - уже изменен
if:
return res
else:
# умножаем на*input^
# но число раз = 1
return n * res
ρ-метод Полларда
## SOLVE
# *********************************************************
def solve:
# g**x = a mod p
n = EulerPhi
'''
использование Функции Эйлера дает возможность
работать не только для простых p
'''
a1 = 0
a2 = 0
b1 = 0
b2 = 0
x1 = 1
x2 = 1
if:
return
start = True
while:
start = False
'''
Поиск совпадающих xi и x2i
использован алгоритм
похожий на этот
http://en.wikipedia.org/wiki/Pollard%27s_rho_algorithm_for_logarithms
'''
'''
xi ← f,
ai ← g,
bi ← h
'''
if:
x1 = mod
a1 = a1
b1 = mod
if:
x1 = mod
a1 = mod
b1 = mod
if:
x1 = mod
a1 = mod
b1 = b1
for i in xrange:
'''
x2i ← f),
a2i ← g,g),
b2i ← h,h)
'''
if:
x2 = mod
a2 = a2
b2 = mod
if:
x2 = mod
a2 = mod
b2 = mod
if:
x2 = mod
a2 = mod
b2 = b2
u = mod
v = mod
if == 0 ):
return
'''
В питоне можно возвращать
не одно значение,
а несколько
'''
d, nu, mu = ExtendedGCD
'''
nu = v^ mod n
'''
x = None
i = 0
while):
'''
Это наименее эффективная реализация
алгоритма Полларда,
g^u == a^v mod p
g^ = a^ = a ^ = a^ = g mod p
xd = u * nu + w * n
далее использован перебор,
правда значительно меньшего размера
чем в premutive_log
Проблема в том, что нужно правильно подобрать w
'''
w = i
x = /d) % n
# тут иcпользован % вместо mod
# потому что в длинных выражениях '%' виднее
if % p == 0 ):
return
i += 1
return
Наивный Алгоритм
## PREMUTIVE_LOG
# *********************************************************
def premutive_log:
'''
Поиск дискретного логарифма перебором
использовалась для тестирования
'''
x = 0
while:
if%b == 0):
'''если разность делится на b '''
return x
x += 1
return None
Проверка
## TEST
# *********************************************************
def test:
'''
Функция для тестирования
'''
g = 3
a = 13
m = 25
print solve
print premutive_log
Просмотров: 1619
|
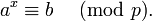
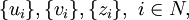
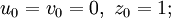
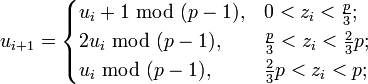
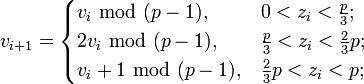
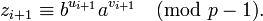
 и ищется номер i, для которого zi = z2i. Для такого i выполнено
и ищется номер i, для которого zi = z2i. Для такого i выполнено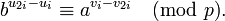
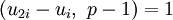 , то
, то