Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Поточный шифр - Криптоанализ. Атаки на поточные шифры22 января 2011Оглавление: 1. Поточный шифр 2. Режим гаммирования для поточных шифров 3. Классификация поточных шифров 4. Поточные шифры на регистрах сдвига с линейной обратной связью 5. Потоковые шифры основанные на РСЛОС. Усложнение 6. Основные отличия поточных шифров от блочных 7. Проектирование поточных шифров 8. Криптоанализ. Атаки на поточные шифры Все методы криптоанализа поточных шифров обычно подразделяют на силовые, статистические и аналитические. Силовые атакиК этому классу относятся атаки, осуществляющие полный перебор всех возможных вариантов. Сложность полного перебора зависит от количества всех возможных решений задачи. Этот класс атак применим ко всем видам систем поточного шифрования. При разработке систем шифрования разработчики стремятся сделать так, чтобы этот вид атак был наиболее эффективным по сравнению с другими существующими методами взлома. Статистические атакиСтатистические атаки делятся на два подкласса:
Оба метода используют принцип линейной сложности. Аналитические атакиЭтот вид атак рассматривается в предположении, что криптоаналитику известны описание генератора, открытый и соответствующий закрытый тексты. Задача криптоаналитика определить использованный ключ. Виды аналитических атак, применяемые к синхронным поточным шифрам:
Корреляционные атакиЯвляются наиболее распространёнными атаками для взлома поточных шифров. Известно, что работа по вскрытию криптосистемы может быть значительно сокращена, если нелинейная функция пропускает на выход информацию о внутренних компонентах генератора. Поэтому для восстановления начального заполнения регистров корреляционные атаки исследуют корреляцию выходной последовательности шифросистемы с выходной последовательностью регистров. Существуют следующие подклассы корреляционных атак:
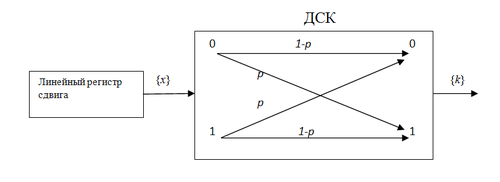
Схема базовой корреляционной атаки
Рассмотрим на примере базовой корреляционной атаки Зигенталера, которая основана на понятии расстояния Хэмминга между двумя двоичными последовательностями одинаковой длины. Применима к комбинирующим генераторам. Для выявления влияния j-го линейного регистра сдвига. Алгоритм атаки состоит из двух этапов:
В случае успеха при сравнении, фаза называется верной и происходит переход к следующему регистру Теперь немного о подборе порогового значения Например, выбрали
Примером этого покласса атак может служить быстрая корреляционная атака Майера и Штаффельбаха. Применима она как к фильтр-генераторам, так и комбинирующим генераторам и является базовой для всех остальных быстрых корреляционных атак данного типа. Идея атаки основывается на использовании уравнений проверки четности для полинома обратной связи линейного регистра.
Под быстрыми корреляционными атаками подразумеваются атаки, вычислительная сложность которых значительно меньше вычислительной сложности силовых атак. Компромисс «время-память»Цель данной атаки — восстановление исходного состояния регистра сдвига, используя известную схема устройства и фрагмент шифрующей последовательности. Сложность атаки зависит от размера шифра и длины перехваченной гаммы. Состоит из двух этапов:
Примерами этого класса атак являются атака Стива Беббиджа и атака Бирюкова-Шамира. «Предполагай и определяй»Атака основывается на предположении, что криптоаналитику известны гамма, полином обратной связи, количество сдвигов регистра между выходами схемы и фильтрующая функция. Состоит из трёх этапов:
Сложность алгоритма зависит от устройства генератора и от количества предположений. Просмотров: 15994
|
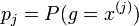 исходя из комбинирующей функции
исходя из комбинирующей функции 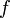 и второго этапа.
и второго этапа.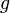 с соответствующим фрагментом из
с соответствующим фрагментом из 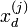 , путём вычисления функции кросс-корреляции
, путём вычисления функции кросс-корреляции 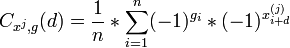 и сравнения этого значения с некоторым числом
и сравнения этого значения с некоторым числом 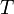 .
.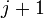 . Иначе, фаза называется неверной и переходят к
. Иначе, фаза называется неверной и переходят к 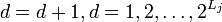 . Выходными значениями этого алгоритма являются состояния
. Выходными значениями этого алгоритма являются состояния 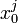 , вносящие информацию в гамму.
, вносящие информацию в гамму.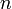 : Задаём нужные нам вероятности «ложной тревоги»
: Задаём нужные нам вероятности «ложной тревоги» 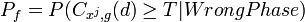 и пропуска истинного начального заполнения
и пропуска истинного начального заполнения 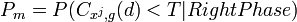 .
.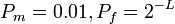 , где
, где 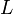 - длина регистра. А затем из этих условий находим
- длина регистра. А затем из этих условий находим 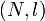 линейного кода. Аналогично базовым корреляционным атакам, этот подкласс использует понятие расстояния Хэмминга.
линейного кода. Аналогично базовым корреляционным атакам, этот подкласс использует понятие расстояния Хэмминга.