Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Параметрическое задание поверхности23 января 2011Оглавление: 1. Параметрическое задание поверхности 2. Кривые поверхности 3. Свойства параметрических поверхностей Класс трёхмерных параметрических поверхностей определяется функцией Наиболее практичным является случай, когда множество
Параметрические поверхности широко используются в прикладной геометрии и компьютерной графике для представления сложных поверхностей. Параметризация делает такие поверхности удобными для обработки и отображения. Параметризация простейших поверхностей
Точка
В общем случае параметризацию в N-угольнике можно ввести используя систему барицентрических координат.
Этот важнейший частный случай N-угольника заслуживает особого внимания. Наиболее распространённый способ параметризации треугольника - линейное отображение на него треугольника из uv-пространства.
Для параметризации сферы удобнее всего использовать одноимённую систему координат:
Вполне естественно использовать цилиндрическую систему координат:
Просмотров: 4493
|
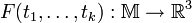 , зависящей от k параметров и отображающей некоторое связное множество
, зависящей от k параметров и отображающей некоторое связное множество 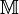 из n-мерного пространства в трёхмерное пространство таким образом, что это отображение является поверхностью. Эта функция F задаёт класс поверхностей, а набор k параметров - конкретную поверхность из этого класса.
из n-мерного пространства в трёхмерное пространство таким образом, что это отображение является поверхностью. Эта функция F задаёт класс поверхностей, а набор k параметров - конкретную поверхность из этого класса.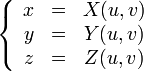 , где
, где 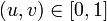
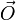 и базис из двух неколлинеарных векторов
и базис из двух неколлинеарных векторов 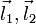 в трёхмерном пространстве определяет плоскость и отображение на неё двумерной декартовой системы координат. Тем самым определяется uv-параметризация плоскости:
в трёхмерном пространстве определяет плоскость и отображение на неё двумерной декартовой системы координат. Тем самым определяется uv-параметризация плоскости: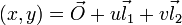
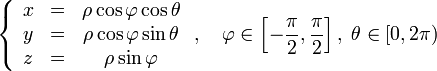 .
.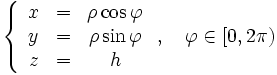 .
.