Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Односторонняя функция - Кандидаты в односторонние функции22 января 2011Оглавление: 1. Односторонняя функция 2. Определение 3. Односторонние функции в криптографических схемах 4. Кандидаты в односторонние функции Далее описаны несколько претендентов на односторонние функции. Честно говоря, не известно, являются ли они действительно односторонними. Но обширные исследования пока не смогли найти эффективный обратный алгоритм к каждой из них. Умножение и факторизацияФункция f принимает на вход два простых числа p и q в двоичном представлении и возвращает их произведение. Эта функция может быть вычислена за время порядка O, где n — общая длина входных данных. Построение обратной функции требует нахождения множителей заданного целого числа N. Лучший известный алгоритм разложения на множители выполняется за время Функция может быть обобщена на диапазон полупростых чисел. Заметим, что f не сможет быть односторонней для произвольных p, q > 1, так как их произведение с вероятностью ¾ имеет множитель 2. Возведение в квадрат и извлечение квадратного корня по модулюФункция f принимает два целых числа x и N, где N — произведение двух простых p и q. На выходе — остаток от деления x на N. Нахождение обратной функции требует вычисления квадратного корня по модулю N, то есть x если известно y и x mod N = y. Можно показать, что последняя задача вычислительно так же сложна, как и разложение N на множители. Криптосистема Рабина основывается на предположении, что функция Рабина является односторонней. Дискретное экспоненцирование и логарифмированиеФункция дискретного экспоненцирования f принимает в качестве аргументов простое число p и целое x в интервале от 0 до p−1 и возвращает остаток от деления 2 на p. Эта функция может быть легко вычислена за время O, где n — количество битов в p. Обращение этой функции требует вычисления дискретного логарифма по модулю p. То есть, по заданному простому p и целому y между 0 и p−1 требуется найти такое x, что 2 mod p = y. Схема Эль-Гамаля основывается на этой функции. Криптографические хэш-функцииСуществует множество криптографических хэш-функций, которые быстро вычисляются. Некоторые из более простых версий не проходили сложный анализ, но самые сильные версии продолжают предлагать быстрые практические решения для односторонних вычислений. Большая часть теоретической поддержки этих функций направлена на срыв некоторых из ранее проведенных успешных атак. Другие претендентыДругие претенденты в односторонние функции основываются на сложности декодирования случайных линейных кодов и иных задачах. Просмотров: 4303
|
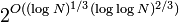 и является псевдополиномиальным.
и является псевдополиномиальным.