Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Нейронная сеть Кохонена23 января 2011Оглавление: 1. Нейронная сеть Кохонена 2. Сети векторного квантования 3. Самоорганизующиеся карты Кохонена 4. Упругие карты 5. Сети векторного квантования, обучаемые с учителем класс нейронных сетей, основным элементом которых является слой Кохонена. Слой Кохонена состоит из адаптивных линейных сумматоров. Как правило, выходные сигналы слоя Кохонена обрабатываются по правилу «победитель забирает всё»: наибольший сигнал превращается в единичный, остальные обращаются в ноль. По способам настройки входных весов сумматоров и по решаемым задачам различают много разновидностей сетей Кохонена. Наиболее известные из них:
Слой КохоненаБазовая версияСлой Кохонена состоит из некоторого количества n параллельно действующих линейных элементов. Все они имеют одинаковое число входов m и получают на свои входы один и тот же вектор входных сигналов x =. На выходе jго линейного элемента получаем сигнал где wji — весовой коэффициент iго входа jго нейрона, wj0 — пороговый коэффициент. После прохождения слоя линейных элементов сигналы посылаются на обработку по правилу «победитель забирает всё»: среди выходных сигналов yj ищется максимальный; его номер jmax = argmaxj{yj}. Окончательно, на выходе сигнал с номером jmax равен единице, остальные — нулю. Если максимум одновременно достигается для нескольких jmax, то либо принимают все соответствующие сигналы равными единице, либо только первый в списке. «Нейроны Кохонена можно воспринимать как набор электрических лампочек, так что для любого входного вектора загорается одна из них.» Геометрическая интерпретация
Разбиение плоскости на многоугольники Вороного-Дирихле для случайно выбранных точек.
Большое распространение получили слои Кохонена, построенные следующим образом: каждому нейрону сопоставляется точка Wj = в m-мерном пространстве. Для входного вектора x = вычисляются его евклидовы расстояния ρj до точек Wj и «ближайший получает всё» — тот нейрон, для которого это расстояние минимально, выдаёт единицу, остальные — нули. Следует заметить, что для сравнения расстояний достаточно вычислять линейную функцию сигнала: . Последнее слагаемое Таким образом, координаты точки Wj = совпадают с весами линейного нейрона слоя Кохонена. Если заданы точки Wj =, то m-мерное пространство разбивается на соответствующие многогранники Вороного-Дирихле Vj: многогранник Vj состоит из точек, которые ближе к Wj, чем к другим Wk. Просмотров: 7206
|
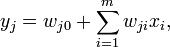
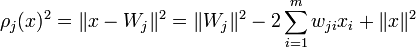
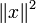 одинаково для всех нейронов, поэтому для нахождения ближайшей точки оно не нужно. Задача сводится к поиску номера наибольшего из значений линейных функций:
одинаково для всех нейронов, поэтому для нахождения ближайшей точки оно не нужно. Задача сводится к поиску номера наибольшего из значений линейных функций: