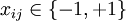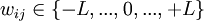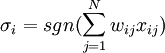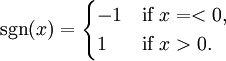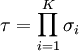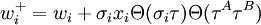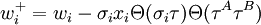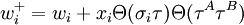Нейрокриптография - Протокол обмена ключами

Интернет магазин китайских планшетных компьютеров

Компьютеры - Нейрокриптография - Протокол обмена ключами

22 января 2011

Оглавление:
1. Нейрокриптография
2. Применение
3. Протокол обмена ключами

Для обмена ключами между двумя абонентами наиболее часто используется алгоритм Диффи-Хеллмана. Его более безопасная замена основана на синхронизации двух древовидных машин четности. Синхронизация этих машин похожа на синхронизацию двух хаотических осцилляторов в теории хаотических связей.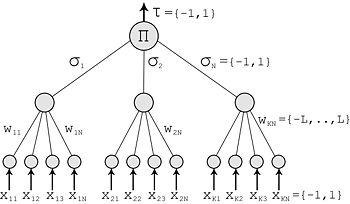

TPM

TPM — это особый вид многоуровневой нейронной сети прямого распространения.

Она состоит из одного выходного нейрона, K скрытых нейронов и K*N входных нейронов. Входные нейроны принимают двоичные значения:

$x_{ij} \in \left\{ -1,+1 \right\}$

Веса между входными и скрытыми нейронами принимают значения:

$w_{ij} \in \left\{-L,...,0,...,+L \right\}$

Значение каждого скрытого нейрона есть сумма произведений входного значения и весового коэффициента:

$\sigma_i=sgn$

$\sgn = \begin{cases} -1 & \text{if } x =< 0, \\ 1 & \text{if } x > 0. \end{cases}$

Значение выходного нейрона есть произведение всех скрытых нейронов:

$\tau=\prod_{i=1}^{K}\sigma_i$

Выходное значение также двоичное.

Протокол

У каждого абонента есть своя TPM. Их синхронизация происходит следующим образом:

Задаём случайные значения весовых коэффициентов
Выполняем следующие шаги, пока не наступит синхронизация
1. Генерируем случайный входной вектор X
2. Вычисляем значения скрытых нейронов
3. Вычисляем значение выходного нейрона
4. Сравниваем выходы двух TPM:
  1. Выходы разные: переход к п.2.1
  2. Выходы одинаковые: применяем выбранное правило к весовым коэффициентам

После полной синхронизации, А и Б могут использовать веса в качестве ключа.

Этот метод известен как двунаправленное обучение.

Для обновления весовых коэффициентов могут использоваться следующие правила:

Правило Хеббиана:

$w_i^+=w_i+\sigma_ix_i\Theta\Theta$

Анти-правило Хеббиана:

$w_i^+=w_i-\sigma_ix_i\Theta\Theta$

Случайное блуждание:

$w_i^+=w_i+x_i\Theta\Theta$

Виды атак и надёжность

Для каждой атаки предполагается, что криптоаналитик Е может подслушивать сообщения между А и Б, но не может их изменять.

Метод грубой силы

Криптоаналитик должен проверить все возможные варианты ключей, то есть все возможные веса w_ij. Если имеется K скрытых нейронов, K*N входных нейронов и максимальный вес L, то это даёт вариантов. Например, для K = 3, L = 3, N = 100 ≈3*10 различных ключей. На сегодняшний день такая атака невозможна.

Обучение собственной TPM

Пусть у криптоаналитика есть такая же TPM, как и у абонентов. Он хочет её синхронизировать с двумя другими TPM. На каждом шаге возможны три ситуации:

Output ≠ Output: Абоненты не обновляют веса.
Output = Output = Output: Все трое обновляют веса.
Output = Output ≠ Output: А и Б обновляют веса, но Е не может этого сделать. Поэтому он обучается медленнее, чем А и Б синхронизируются.

Таким образом, криптоаналитик может определить ключ лишь с очень малой вероятностью.

Другие атаки

Защищенность обычных криптографических систем можно улучшить, увеличив длину ключа. В нейрокриптографии вместо ключа увеличивается синаптическая длина L. Это увеличивает сложность атаки экспоненциально, в то время как затраты абонентов на дешифрацию растут полиномиально. Таким образом, взлом подобной системы является NP-сложной задачей.

Алексанр Климов, Антон Митягин и Ади Шамир утверждают, что исходный алгоритм нейросинхронизации может быть сломан по крайней мере тремя видами атак: геометрической, вероятностным анализом и генетическими алгоритмами. Хотя данная реализация небезопасна, идеи случайной синхронизации могут привести к абсолютно безопасной схеме.

Генетическая атака

Атака строится на создании большой популяции нейронных шифровальных устройств — таких же нейросетей с абсолютно идентичной структурой, что А и Б. В процессе обмена информацией между абонентами происходит либо отсеивание ненужных НШУ, либо наоборот — наращивание потенциально благоприятных для взлома. Формализованный алгоритм выглядит так:

Взломщик инициализует свою машину только с одной НШУ. Веса для него выбираются случайно. Также устанавливается некоторое число М — порог популяции НШУ, которое может себе позволить взломщик.
Затем при обмене информацией между А и Б могут возникнуть три ситуации:

1. Если выходные значения А и Б не равны между собой: Output ≠ Output, обновление весов не происходит. Взломщик не трогает свою популяцию.
2. Если Output = Output и число шифровальных устройств у взломщика не превышает порог М, то все НШУ заменяются на репрезентацию из F новых НШУ, каждая из которых получается альтернативной заменой скрытого нейрона на противоположное значение, собственно для этого подбираются новые веса. Затем происходит обучение по правилам Хеббиана.
3. Если Output = Output и число шифровальных устройств у взломщика превышает порог М, то удаляются все те нейромашины, выходное значение которых Output ≠ Output.
Данный алгоритм действует только на маленьких нейросетях и становится в тупик даже на очень мощных компьютерах при K>=6. Строго говоря, все атаки, предложенные Александром Климовым и Антоном Митягиным основаны на том, что НШУ имеет небольшой размер. На практике же редко применяются шифровальные нейросети с параметрами N<100, K<100, L<10.

Защита от квантовых компьютеров

В квантовом компьютере данные хранятся в кубитах. Это позволяет решать более сложные задачи за существенно меньшее время. Поэтому очень важно найти алгоритмы, не основанные на этих проблемах теории чисел.

Нейронный протокол обмена ключей не основан на теории чисел, он основан на различии между однонаправленной и двунаправленной синхронизацией нейронных сетей. Поэтому, подобные протоколы могут ускорить процесс обмена.

<<< Незаконное число

Односторонняя функция >>>

Компьютерное аппаратное обеспечение
Вычислительные комплексы
Компьютерные данные
Компьютерные журналы
Классы компьютеров
Компьютеры

Программное обеспечение
Производители компьютеров
Профессии в ИТ
Системное администрирование
Компьютерный сленг
Списки компьютерных терминов

Человеко-компьютерное взаимодействие