|
|
|
27 апреля 2011
Оглавление:
1. N-Hash
2. Использование
3. Особенности N-Hash
4. Цели N-Hash
5. Алгоритм
6. Безопасность хеш-функций
7. Итоги
Алгоритм N-Hash основан на циклическом повторении операций. На входе имеется хеш-код h0 и он может быть произвольным, на выходе получается хеш-код h сообщения M, которое необходимо хешировать. При этом размер выходящего хеш-кода фиксирован и равен 128 бит, тогда как размер M произволен.
Основные обозначения
- M — сообщение, которое необходимо хешировать;
- Mi — блок сообщения длиной 128 бит. Для того, чтобы хешировать сообщение M необходимо поделить его на блоки Mi;
- hi — хеш-код i-ого шага;
- ν = 1010...1010 — константа, длиной 128 бит;
- | | — конкатенация;
- Vj = δ | | Aj1 | | δ | | Aj2 | | δ | | Aj3 | | δ | | Aj4 | | , где Ajk = 4 * + k, где k=1, 2, 3, 4; δ = 00..00, длиной 24 бит;
- EXG — функция, которая меняет местами старшие и младшие разряды;
- PS — преобразующая функция;
Описание алгоритма
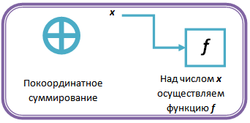
На схеме справа представлены схематические обозначения операций, которые присутствуют на нижеследующих схемах.
- Покоординатное суммирование означает сложение по модулю 2;
- Если x поступает на вход функции f, то на выходе получается f.
Один цикл работы N-Hash
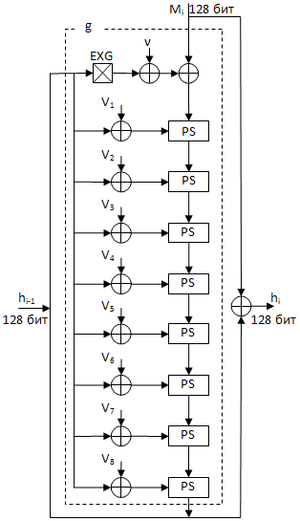
один цикл работы N-Hash
Ниже представлен один цикл работы алгоритма N-Hash.
- На вход функции g подается хеш-код-ого шага hi − 1 и i-ый блок сообщения Mi. При этом h0 выбирается произвольно: например, он может быть нулевым. А также hi − 1 подается на выход на операцию сложения по модулю 2, то есть результат будет выглядеть так:
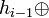 . .
- Из схемы видно, что Mi подается не только на XOR, но и на выход на операцию сложения по модулю 2. То есть теперь в соответствие с первым пунктом результат выглядит таким образом:
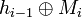 . .
Оставшееся пока неизвестным нечто находится после прохождения каскада из восьми преобразующих функций. Его получение может быть описано таким образом:
- Функция EXG меняет местами старшие и младшие разряды hi − 1 и прибавляет к результату ν, после чего результат складывает по модулю 2 с Mi.
- Как видно из схемы, результат подается последовательно на входы j преобразующих функций, вторым аргументом которых является сумма
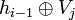 , где j=1, … , 8. , где j=1, … , 8.
- В результате получается хеш-код i-ого шага hi:
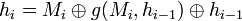 . .
Преобразующая функция
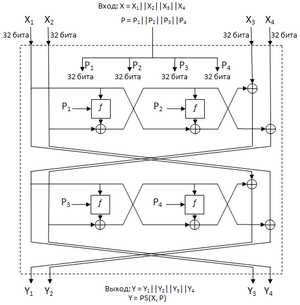
Схема преобразующей функции. Каждый из аргументов разбивается на 4 блока по 32 бит каждый.
Возникает вопрос, как действует преобразующая функция PS.
Рассмотрим верхнюю часть схемы до перекрестья.
Исходное сообщение 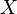 разбивается на блоки по 128 / 4 = 32 бита. разбивается на блоки по 128 / 4 = 32 бита.
Будем считать промежуточными выходами входы в нижнюю часть схемы. 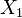 и и 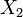 подаются на промежуточные выходы, а на два других выхода подаются операции подаются на промежуточные выходы, а на два других выхода подаются операции 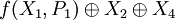 и и 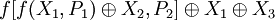 . Теперь можно результаты на промежуточных выходах переобозначить и через них, аналогично верхней части, найти результаты на выходе нижней части, то есть и всей схемы в целом. . Теперь можно результаты на промежуточных выходах переобозначить и через них, аналогично верхней части, найти результаты на выходе нижней части, то есть и всей схемы в целом.
Сделав все необходимые вычисления, получим, что при подаче на вход 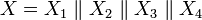 сообщение на выходе сообщение на выходе 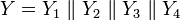 можно представить как конкатенацию сообщений можно представить как конкатенацию сообщений
Поиск функции f
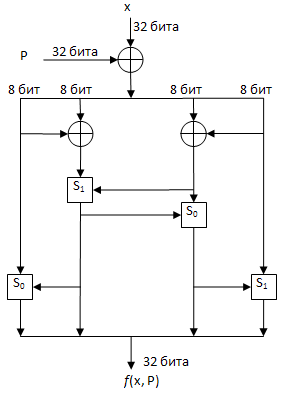
Схема поиска функции f
Так как функция f работает с аргументами, длина которых составляет 32 бит, то из схемы поиска функции f имеем:
- Величину
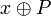 разбиваем на части по 8 бит. разбиваем на части по 8 бит.
- Запишем эти части как
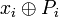 , i=1,…,4 и введет новые обозначения: , i=1,…,4 и введет новые обозначения:
Аргументами функции 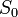 являются являются 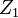 и и 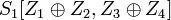 . .
Аргументами функции 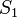 являются являются 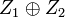 и и 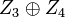 . .
То есть две составляющие части из сообщения на выходе уже известны и равны
-
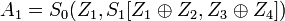 ; ;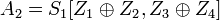 ; ;
Далее будем пользоваться уже полученными оставляющими частями сообщения на выходе для удобства записи:
-
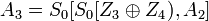 ; ;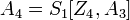 ; ;
- Тогда сообщение на выходе можно представить в виде
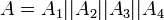 . .
- Причём известно, что
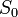 = mod 256 = mod 256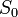 = mod 256 = mod 256
Просмотров: 6713
|



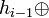 .
.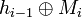 .
.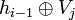 , где j=1, … , 8.
, где j=1, … , 8.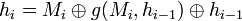 .
.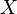 разбивается на блоки по 128 / 4 = 32 бита.
разбивается на блоки по 128 / 4 = 32 бита.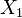 и
и 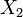 подаются на промежуточные выходы, а на два других выхода подаются операции
подаются на промежуточные выходы, а на два других выхода подаются операции 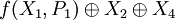 и
и 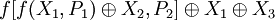 . Теперь можно результаты на промежуточных выходах переобозначить и через них, аналогично верхней части, найти результаты на выходе нижней части, то есть и всей схемы в целом.
. Теперь можно результаты на промежуточных выходах переобозначить и через них, аналогично верхней части, найти результаты на выходе нижней части, то есть и всей схемы в целом.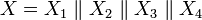 сообщение на выходе
сообщение на выходе 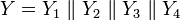 можно представить как конкатенацию сообщений
можно представить как конкатенацию сообщений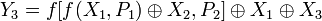 ;
;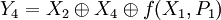 ;
;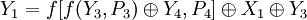 ;
;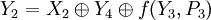 .
.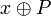 разбиваем на части по 8 бит.
разбиваем на части по 8 бит.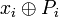 , i=1,…,4 и введет новые обозначения:
, i=1,…,4 и введет новые обозначения:
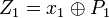 ;
;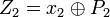 ;
;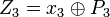 ;
;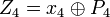 ;
;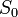 являются
являются 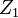 и
и 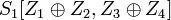 .
.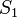 являются
являются 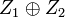 и
и 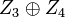 .
.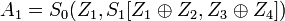 ;
;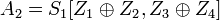 ;
;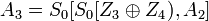 ;
;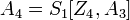 ;
;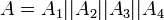 .
.