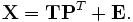Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Метод главных компонент - Специальная терминология22 января 2011Оглавление: 1. Метод главных компонент 2. Формальная постановка задачи 3. Диагонализация ковариационной матрицы 4. Сингулярное разложение матрицы данных 5. Матрица преобразования к главным компонентам 6. Отбор главных компонент по правилу Кайзера 7. Оценка числа главных компонент по правилу сломанной трости 8. Нормировка 9. Механическая аналогия и метод главных компонент для взвешенных данных 10. Специальная терминология 11. Примеры использования В статистике при использовании метода главных компонент используют несколько специальных терминов. Матрица данных Матрица нагрузок Матрица счетов Матрица Z-счетов Матрица ошибок Основная формула: Пределы применимости и ограничения эффективности метода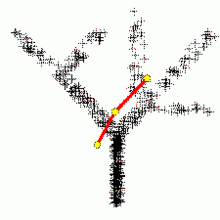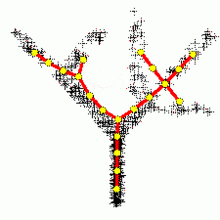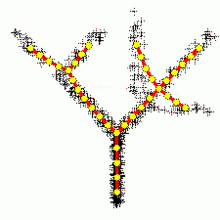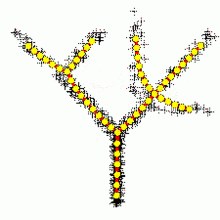
Построение ветвящихся главных компонент методом топологических грамматик. Крестики — точки данных, красное дерево с желтыми узлами — аппроксимирующий дендрит.
Метод главных компонент применим всегда. Распространённое утверждение о том, что он применим только к нормально распределённым данным неверно: в исходной формулировке К. Пирсона ставится задача об аппроксимации конечного множества данных и отсутствует даже гипотеза о их статистическом порождении, не говоря уж о распределении. Однако метод не всегда эффективно снижает размерность при заданных ограничениях на точность δk. Прямые и плоскости не всегда обеспечивают хорошую аппроксимацию. Например, данные могут с хорошей точностью следовать какой-нибудь кривой, а эта кривая может быть сложно расположена в пространстве данных. В этом случае метод главных компонент для приемлемой точности потребует нескольких компонент, или вообще не даст снижения размерности при приемлемой точности. Для работы с такими «кривыми» главными компонентами изобретен метод главных многообразий и различные версии нелинейного метода главных компонент. Больше неприятностей могут доставить данные сложной топологии. Для их аппроксимации также изобретены различные методы, например самоорганизующиеся карты Кохонена, нейронный газ или топологические грамматики. Если данные статистически порождены с распределением, сильно отличающимся от нормального, то для аппроксимации распределения полезно перейти от главных компонент к независимым компонентам, которые уже не ортогональны в исходном скалярном произведении. Наконец, для изотропного распределения вместо эллипсоида рассеяния получаем шар, и уменьшить размерность методами аппроксимации невозможно. Просмотров: 23880
|
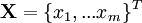 ; каждая строка — вектор предобработанных данных, число строк — m, число столбцов — n;
; каждая строка — вектор предобработанных данных, число строк — m, число столбцов — n;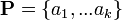 ; каждый столбец — вектор главных компонент, число строк — n, число столбцов — k;
; каждый столбец — вектор главных компонент, число строк — n, число столбцов — k;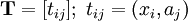 ; каждая строка — проекция вектора данных на k главных компонент; число строк — m, число столбцов — k;
; каждая строка — проекция вектора данных на k главных компонент; число строк — m, число столбцов — k;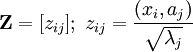 ; каждая строка — проекция вектора данных на k главных компонент, нормированная на единичную выборочную дисперсию; число строк — m, число столбцов — k;
; каждая строка — проекция вектора данных на k главных компонент, нормированная на единичную выборочную дисперсию; число строк — m, число столбцов — k;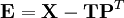 .
.