Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Метод главных компонент - Нормировка22 января 2011Оглавление: 1. Метод главных компонент 2. Формальная постановка задачи 3. Диагонализация ковариационной матрицы 4. Сингулярное разложение матрицы данных 5. Матрица преобразования к главным компонентам 6. Отбор главных компонент по правилу Кайзера 7. Оценка числа главных компонент по правилу сломанной трости 8. Нормировка 9. Механическая аналогия и метод главных компонент для взвешенных данных 10. Специальная терминология 11. Примеры использования Нормировка после приведения к главным компонентамПосле проецирования на первые k главных компонент с
Именно это преобразование чаще всего называется преобразованием Кархунена-Лоэва. Здесь ai — векторы-столбцы, а верхний индекс T означает транспонирование. Нормировка до вычисления главных компонентПредупреждение: не следует путать нормировку, проводимую после преобразования к главным компонентам, с нормировкой и «обезразмериванием» при предобработке данных, проводимой до вычисления главных компонент. Предварительная нормировка нужна для обоснованного выбора метрики, в которой будет вычисляться наилучшая аппроксимация данных, или будут искаться направления наибольшего разброса. Например, если данные представляют собой трёхмерные векторы из «метров, литров и килограмм», то при использовании стандартного евклидового расстояния разница в 1 метр по первой координате будет вносить тот же вклад, что разница в 1 литр по второй, или в 1 кг по третьей. Обычно системы единиц, в которых представлены исходные данные, недостаточно точно отображают наши представления о естественных масштабах по осям, и проводится «обезразмеривание»: каждая координата делится на некоторый масштаб, определяемый данными, целями их обработки и процессами измерения и сбора данных. Есть три cущественно различных стандартных подхода к такой нормировке: на единичную дисперсию по осям, на равную точность измерения и на равные требования в задаче. На выбор предобработки влияют содержательная постановка задачи, а также условия сбора данных. Предварительная нормировка на единичную дисперсию по осям разрушается поворотом системы координат, если оси не являются главными компонентами, и нормировка при предобработке данных не заменяет нормировку после приведения к главным компонентам. Просмотров: 23939
|
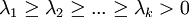 удобно произвести нормировку на единичную дисперсию по осям. Дисперсия вдоль iй главной компоненты равна
удобно произвести нормировку на единичную дисперсию по осям. Дисперсия вдоль iй главной компоненты равна 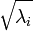 . Это преобразование не является ортогональным и не сохраняет скалярного произведения. Ковариационная матрица проекции данных после нормировки становится единичной, проекции на любые два ортогональных направления становятся независимыми величинами, а любой ортонормированный базис становится базисом главных компонент. Отображение из пространства исходных данных на первые k главных компонент вместе с нормировкой задается матрицей
. Это преобразование не является ортогональным и не сохраняет скалярного произведения. Ковариационная матрица проекции данных после нормировки становится единичной, проекции на любые два ортогональных направления становятся независимыми величинами, а любой ортонормированный базис становится базисом главных компонент. Отображение из пространства исходных данных на первые k главных компонент вместе с нормировкой задается матрицей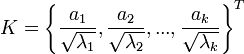 .
.