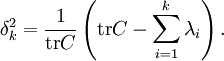Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Метод главных компонент - Матрица преобразования к главным компонентам22 января 2011Оглавление: 1. Метод главных компонент 2. Формальная постановка задачи 3. Диагонализация ковариационной матрицы 4. Сингулярное разложение матрицы данных 5. Матрица преобразования к главным компонентам 6. Отбор главных компонент по правилу Кайзера 7. Оценка числа главных компонент по правилу сломанной трости 8. Нормировка 9. Механическая аналогия и метод главных компонент для взвешенных данных 10. Специальная терминология 11. Примеры использования Матрица A преобразования данных к главным компонентам строится из векторов главных компонент: После преобразования большая часть вариации данных будет сосредоточена в первых координатах, что даёт возможность отбросить оставшиеся и рассмотреть пространство уменьшенной размерности. Остаточная дисперсияПусть данные центрированы, где Эта величина называется остаточной дисперсией. Величина называется объяснённой дисперсией. Их сумма равна выборочной дисперсии. Соответствующий квадрат относительной ошибки — это отношение остаточной дисперсии к выборочной дисперсии: По относительной ошибке δk оценивается применимость метода главных компонент с проецированием на первые k компонент. Замечание: в большинстве вычислительных алгоритмов собственные числа λi с соответствующими собственными векторами — главными компонентами ai вычисляются в порядке «от больших λi — к меньшим». Для вычисления δk достаточно вычислить первые k собственных чисел и след эмпирической ковариационной матрицы C, Просмотров: 23876
|
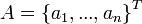 . Здесь ai — ортонормированные векторы-столбцы главных компонент, расположенные в порядке убывания собственных значений, верхний индекс T означает транспонирование. Матрица A является ортогональной: AA = 1.
. Здесь ai — ортонормированные векторы-столбцы главных компонент, расположенные в порядке убывания собственных значений, верхний индекс T означает транспонирование. Матрица A является ортогональной: AA = 1.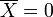 . При замене векторов данных xi на их проекцию на первые k главных компонент
. При замене векторов данных xi на их проекцию на первые k главных компонент 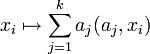 вносится средний квадрат ошибки в расчете на один вектор данных:
вносится средний квадрат ошибки в расчете на один вектор данных: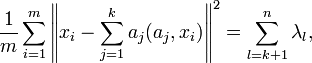
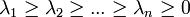 собственные значения эмпирической ковариационной матрицы C, расположенные в порядке убывания, с учетом кратности.
собственные значения эмпирической ковариационной матрицы C, расположенные в порядке убывания, с учетом кратности.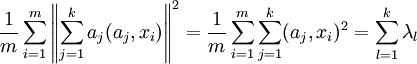
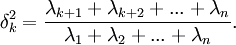
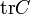 . Тогда
. Тогда