Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Метод главных компонент - Формальная постановка задачи22 января 2011Оглавление: 1. Метод главных компонент 2. Формальная постановка задачи 3. Диагонализация ковариационной матрицы 4. Сингулярное разложение матрицы данных 5. Матрица преобразования к главным компонентам 6. Отбор главных компонент по правилу Кайзера 7. Оценка числа главных компонент по правилу сломанной трости 8. Нормировка 9. Механическая аналогия и метод главных компонент для взвешенных данных 10. Специальная терминология 11. Примеры использования Задача анализа главных компонент, имеет, как минимум, четыре базовых версии:
Первые три версии оперируют конечными множествами данных. Они эквивалентны и не используют никакой гипотезы о статистическом порождении данных. Четвёртая версия оперирует случайными величинами. Конечные множества появляются здесь как выборки из данного распределения, а решение трёх первых задач — как приближение к «истинному» преобразованию Кархунена-Лоэва. При этом возникает дополнительный и не вполне тривиальный вопрос о точности этого приближения. Аппроксимация данных линейными многообразиями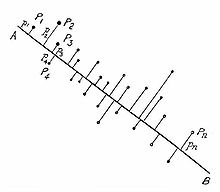
Иллюстрация к знаменитой работе К. Пирсона: даны точки Pi на плоскости, pi — расстояние от Pi до прямой AB. Ищется прямая AB, минимизирующая сумму
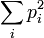 Метод главных компонент начинался с задачи наилучшей аппроксимации конечного множества точек прямыми и плоскостями. Дано конечное множество векторов
где
где
Решение задачи аппроксимации для k = 0,1,...,n − 1 даётся набором вложенных линейных многообразий то есть
Это — выборочное среднее: Векторы главных компонент могут быть найдены как решения однотипных задач оптимизации:
На каждом подготовительном шаге вычитаем проекцию на предшествующую главную компоненту. Найденные векторы Неединственность в определении ak помимо тривиального произвола в выборе знака может быть более существенной и происходить, например, из условий симметрии данных. Последняя главная компонента an — единичный вектор, ортогональный всем предыдущим ak. Поиск ортогональных проекций с наибольшим рассеянием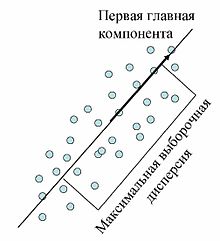
Первая главная компонента максимизирует выборочную дисперсию проекции данных
Пусть нам дан центрированный набор векторов данных
Выборочная дисперсия данных вдоль направления, заданного нормированным вектором ak, это . Решение задачи о наилучшей аппроксимации даёт то же множество главных компонент Поиск ортогональных проекций с наибольшим среднеквадратичным расстоянием между точкамиЕщё одна эквивалентная формулировка следует из очевидного тождества, верного для любых m векторов xi: В левой части этого тождества стоит среднеквадратичное расстояние между точками, а в квадратных скобках справа — выборочная дисперсия. Таким образом, в методе главных компонент ищутся подпространства, в проекции на которые среднеквадратичное расстояние между точками максимально. Такая переформулировка позволяет строить обобщения с взвешиванием различных парных расстояний. Аннулирование корреляций между координатамиДля заданной n-мерной случайной величины X найти такой ортонормированный базис,
Здесь Просмотров: 23874
|
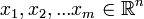 . Для каждого k = 0,1,...,n − 1 среди всех k-мерных линейных многообразий в
. Для каждого k = 0,1,...,n − 1 среди всех k-мерных линейных многообразий в 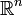 найти такое
найти такое 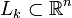 , что сумма квадратов уклонений xi от Lk минимальна:
, что сумма квадратов уклонений xi от Lk минимальна: ,
,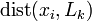 — евклидово расстояние от точки до линейного многообразия. Всякое k-мерное линейное многообразие в
— евклидово расстояние от точки до линейного многообразия. Всякое k-мерное линейное многообразие в 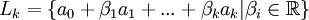 , где параметры βi пробегают вещественную прямую
, где параметры βi пробегают вещественную прямую 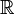 ,
, 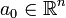 а
а 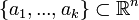 — ортонормированный набор векторов
— ортонормированный набор векторов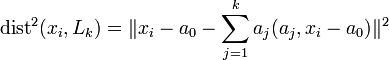 ,
, евклидова норма,
евклидова норма, 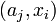 — евклидово скалярное произведение, или в координатной форме:
— евклидово скалярное произведение, или в координатной форме: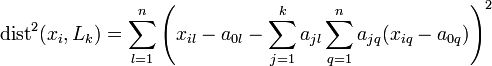 .
.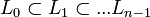 ,
, 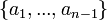 и вектором a0. Вектор a0 ищется, как решение задачи минимизации для L0:
и вектором a0. Вектор a0 ищется, как решение задачи минимизации для L0: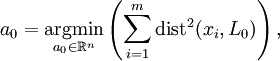
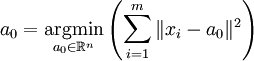 .
.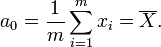 Фреше в 1948 году обратил внимание, что вариационное определение среднего очень удобно для построения статистики в произвольном метрическом пространстве, и построил обобщение классической статистики для общих пространств.
Фреше в 1948 году обратил внимание, что вариационное определение среднего очень удобно для построения статистики в произвольном метрическом пространстве, и построил обобщение классической статистики для общих пространств.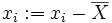 . Теперь
. Теперь 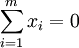 ;
;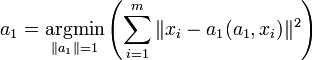 .
.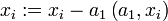 ;
;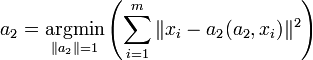 .
. ;
;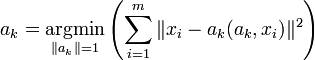 .
.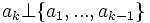 в условия задачи оптимизации.
в условия задачи оптимизации.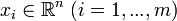 . Задача — найти такое ортогональное преобразование в новую систему координат, для которого были бы верны следующие условия:
. Задача — найти такое ортогональное преобразование в новую систему координат, для которого были бы верны следующие условия: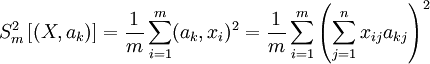
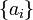 , что и поиск ортогональных проекций с наибольшим рассеянием, по очень простой причине:
, что и поиск ортогональных проекций с наибольшим рассеянием, по очень простой причине: 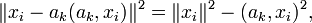 и первое слагаемое не зависит от ak.
и первое слагаемое не зависит от ak.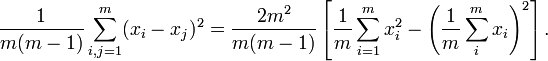
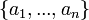 , в котором коэффициент ковариации между различными координатами равен нулю. После преобразования к этому базису
, в котором коэффициент ковариации между различными координатами равен нулю. После преобразования к этому базису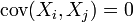 для
для 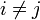 .
.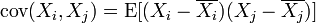 — коэффициент ковариации.
— коэффициент ковариации.