Метод главных компонент - Диагонализация ковариационной матрицы

Интернет магазин китайских планшетных компьютеров

Компьютеры - Метод главных компонент - Диагонализация ковариационной матрицы

22 января 2011

Оглавление:
1. Метод главных компонент
2. Формальная постановка задачи
3. Диагонализация ковариационной матрицы
4. Сингулярное разложение матрицы данных
5. Матрица преобразования к главным компонентам
6. Отбор главных компонент по правилу Кайзера
7. Оценка числа главных компонент по правилу сломанной трости
8. Нормировка
9. Механическая аналогия и метод главных компонент для взвешенных данных
10. Специальная терминология
11. Примеры использования

Все задачи о главных компонентах приводят к задаче диагонализации ковариационной матрицы или выборочной ковариационной матрицы. Эмпирическая или выборочная ковариационная матрица, это

$C =,\ c_{ij} = \frac{1}{m-1} \sum_{l=1}^m.$

Ковариационная матрица многомерной случайной величины X, это

$\Sigma =,\ \sigma_{ij} = \operatorname{cov}=E.$

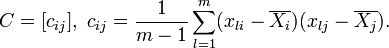
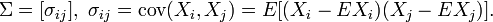
Векторы главных компонент для задач о наилучшей аппроксимации и о поиске ортогональных проекций с наибольшим рассеянием — это ортонормированный набор 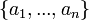$\left\{a_1,..., a_n \right\}$ собственных векторов эмпирической ковариационной матрицы C, расположенных в порядке убывания собственных значений 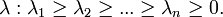$\lambda: \lambda_1 \ge \lambda_2 \ge ... \ge \lambda_n \ge 0.$ Эти векторы служат оценкой для собственных векторов ковариационной матрицы 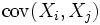$\operatorname{cov}$ . В базисе из собственных векторов ковариационной матрицы она, естественно, диагональна, и в этом базисе коэффициент ковариации между различными координатами равен нулю.

Если спектр ковариационной матрицы вырожден, то выбирают произвольный ортонормированный базис собственных векторов. Он существует всегда, а собственные числа ковариационной матрицы всегда вещественны и неотрицательны.

<<< Инфографика

Нейронная сеть Кохонена >>>

Компьютерное аппаратное обеспечение
Вычислительные комплексы
Компьютерные данные
Компьютерные журналы
Классы компьютеров
Компьютеры

Программное обеспечение
Производители компьютеров
Профессии в ИТ
Системное администрирование
Компьютерный сленг
Списки компьютерных терминов

Человеко-компьютерное взаимодействие