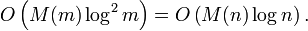Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Метод БВЕ - Детали БВЕ на примере быстрого вычисления константы e23 января 2011Оглавление: 1. Метод БВЕ 2. БВЕ-вычисление классических констант 3. Детали БВЕ на примере быстрого вычисления константы e Для вычисления константы e возьмём
Будем вычислять сумму
за k шагов следующего процесса. Шаг 1. Объединяя слагаемые S последовательно попарно и вынося за скобки "очевидный" общий множитель, получаем
Будем вычислять только целые значения выражений, стоящих в скобках, т.е. значения
Таким образом, на первом шаге сумма S преобразуется к виду
На первом шаге вычисляется только
Далее мы действуем аналогично: объединяя на каждом шаге слагаемые суммы S последовательно попарно, мы выносим за скобки "очевидный" общий множитель и вычисляем только целые значения выражений в скобках. Пусть сделано i шагов такого процесса. Шаг i + 1.
мы вычисляем только
Здесь И т.д. Последний, k -й шаг. Вычисляем одно целое значение α1, вычисляем, пользуясь вышеописанным быстрым алгоритмом, значение !, и производим одно деление целого числа α1 на число ! с точностью до n знаков. Получившийся результат и есть сумма S, или константа e с точностью до 2 . Сложность всех вычислений есть
Просмотров: 2736
|
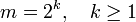 , членов ряда Тейлора для e,
, членов ряда Тейлора для e,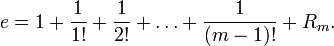 При этом выбираем m так, чтобы для остатка Rm выполнялось неравенство
При этом выбираем m так, чтобы для остатка Rm выполнялось неравенство 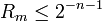 . Это будет, например, когда
. Это будет, например, когда 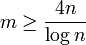 . Таким образом, возьмем m = 2 таким, что натуральное число k определяется неравенствами:
. Таким образом, возьмем m = 2 таким, что натуральное число k определяется неравенствами: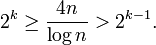
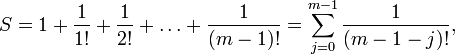
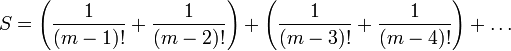
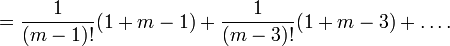
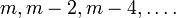
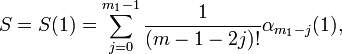
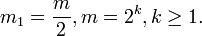
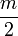 целых чисел вида
целых чисел вида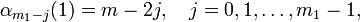
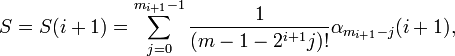
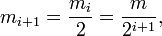
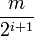 целых чисел вида
целых чисел вида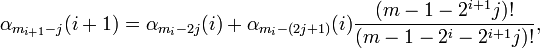
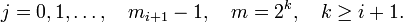
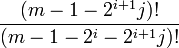 есть произведение 2 целых чисел.
есть произведение 2 целых чисел.