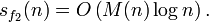Метод БВЕ - БВЕ-вычисление классических констант

Компьютеры - Метод БВЕ - БВЕ-вычисление классических констант

23 января 2011

Оглавление:
1. Метод БВЕ
2. БВЕ-вычисление классических констант
3. Детали БВЕ на примере быстрого вычисления константы e

Для быстрого вычисления константы π можно воспользоваться формулой Эйлера

$\frac{\pi}{4} = \arctan \frac12 + \arctan \frac13,$

и применить БВЕ к суммированию рядов Тейлора для

$\arctan \frac12 = \frac{1}{1*2} - \frac{1}{3*2^3}+ \dots + \frac{^{r-1}}{2^{2r-1}} + R_1 ,$

$\arctan \frac13 = \frac{1}{1*3} - \frac{1}{3*3^3}+ \dots + \frac{^{r-1}}{3^{2r-1}} + R_2 ,$

с остаточными членами R₁, R₂, для которых справедливы оценки

$|R_1| \leq \frac45\frac{1}{2r+1}\frac{1}{2^{2r+1}};$

$|R_2| \leq \frac{9}{10}\frac{1}{2r+1}\frac{1}{3^{2r+1}};$

и при

r = n,

$4 \ < \ 2^{-n}.$

Чтобы вычислить π посредством БВЕ, можно использовать также другие приближения Во всех случаях сложность

s_π = Ologn).

Чтобы вычислить постоянную Эйлера гамма с точностью до n знаков, нужно просуммировать с помощью БВЕ два ряда. А именно, при

$m=6n, \quad k = n, \quad k \geq 1,$

$\gamma = - \log n \sum_{r=0}^{12n} \frac{^rn^{r+1}}{!} + \sum_{r=0}^{12n} \frac{^rn^{r+1}}{!} + O .$

При этом

s_γ = Ologn). Для быстрого вычисления константы γ можно также применить метод БВЕ к другому приближению

С помощью БВЕ можно вычислить быстро следующие два вида рядов:

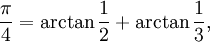
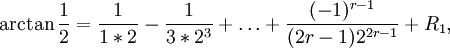
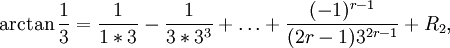
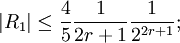
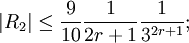
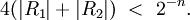
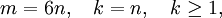
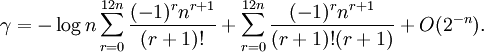
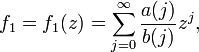
$f_1 = f_1 = \sum_{j=0}^{\infty}\frac{a}{b}z^j ,$

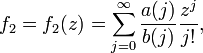
$f_2 = f_2 = \sum_{j=0}^{\infty}\frac{a}{b}\frac{z^j}{j!} ,$

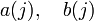при условии, что $a , \quad b$ --- целые числа, 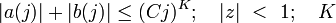$|a|+|b| \leq^K; \quad |z| \ < \ 1; \quad K$ и C есть константы, и z есть алгебраическое число.

Сложность вычисления этих рядов $s_{f_1}= O\left\log^2n \right),$

$s_{f_2}= O\left\log n \right).$