Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Metaball - Способ задания04 мая 2011Оглавление: 1. Metaball 2. Способ задания Каждая управляющая точка определяет собственную n-мерную потенциальную функцию Ui. Затем выбирается некое значение U0, которое определяет форму метасферы. Таким образом, неравенство Часто в качестве функции, задающей метасферу, используют При поиске более эффективной функции потенциала желательно, чтобы она удовлетворяла следующим требованиям:
Простейшая функция потенциала, удовлетворяющая этим критериям: U =, где r – расстояние между управляющей точкой и заданной точкой пространства. Она также довольно эффективна, поскольку не использует деления и извлечения корня. Более сложные модели используют для лучшего сглаживания гауссов потенциал, ограниченный конечным радиусом набора многочленов. Модель мягких объектов братьев Вивилл обеспечивает более высокую степень сглаженности и не использует квадратные корни. Простое обобщение модели можно получить, заменяя расстояние между точками в функции потенциала расстоянием до прямой или расстоянием до поверхности. Есть множество способов рендеринга метасфер. Для трехмерных метасфер чаще всего применяют рэйкастинг и алгоритм marching cubes. Двухмерные метасферы были очень популярны в демосценах в 1990-х. Этот эффект также доступен в модуле XScreensaver. 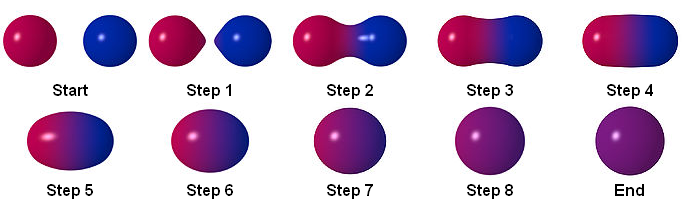
Взаимодействие двух положительных метасфер, смоделированное в Bryce.
Обратите внимание, как две маленьких метасферы сливаются в одну большую. Просмотров: 2027
|
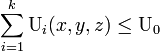 определяет, находится ли точка внутри поверхности, заданной k управляющими точками, или нет.
определяет, находится ли точка внутри поверхности, заданной k управляющими точками, или нет.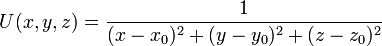 , где — центр метасферы. Однако использование деления делает эту функцию неэффективной по скорости, поэтому обычно ее заменяют аппроксимирующими полиномиальными функциями.
, где — центр метасферы. Однако использование деления делает эту функцию неэффективной по скорости, поэтому обычно ее заменяют аппроксимирующими полиномиальными функциями.