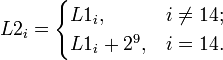Интернет магазин китайских планшетных компьютеров

Компьютеры - MD5 - MD5-хеши

Хеш содержит 128 бит и обычно представляется как последовательность из 32 шестнадцатеричных цифр.

Несколько примеров хеша:

 MD5 = 1bc29b36f623ba82aaf6724fd3b16718

Даже небольшое изменение входного сообщения приводит к полному изменению хеша. Такое свойство алгоритма называется лавинным эффектом.

 MD5 = c93d3bf7a7c4afe94b64e30c2ce39f4f

Пример MD5-хеша для «нулевой» строки:

 MD5 = d41d8cd98f00b204e9800998ecf8427e

Криптоанализ

На данный момент существуют несколько видов «взлома» хешей MD5 — подбора сообщения с заданным хешем:

• Перебор по словарю
• Brute-force
• RainbowCrack

Атаки переборного типа

Для полного перебора или перебора по словарю можно использовать программы PasswordsPro, MD5BFCPF, John the Ripper. Для перебора по словарю существуют готовые словари.

RainbowCrack — еще один метод взлома хеша. Он основан на генерировании большого количества хешей из набора символов, чтобы по получившейся базе вести поиск заданного хеша. Хотя генерация хешей занимает много времени, зато последующий взлом производится очень быстро.

Коллизии MD5

Коллизия хеш-функции — это получение одинакового значения функции для разных сообщений и идентичного начального буфера. В отличие от коллизий, псевдоколлизии определяются как равные значения хеша для разных значений начального буфера, причём сами сообщения могут совпадать или отличаться. В 1996 году Ганс Доббертин нашёл псевдоколлизии в MD5, используя определённые инициализирующие векторы, отличные от стандартных. Оказалось, что можно для известного сообщения построить второе, такое, что оно будет иметь такой же хеш, как и исходное. C точки зрения математики это означает: MD5 = MD5, где IV — начальное значение буфера, а L1 и L2 — различные сообщения. Например, если взять начальное значение буфера:

A = 0x12AC2375
В = 0x3B341042
C = 0x5F62B97C
D = 0x4BA763ED

и задать входное сообщение

то, добавляя число 2 к определённому 32-разрядному слову в блочном буфере, можно получить второе сообщение с таким же хешем. Ханс Доббертин представил такую формулу:

Тогда MD5 = MD5 = BF90E670752AF92B9CE4E3E1B12CF8DE.

В 2004 году китайские исследователи Ван Сяоюнь, Фен Дэнгуо, Лай Сюэцзя и Юй Хунбо объявили об обнаруженной ими уязвимости в алгоритме, позволяющей за небольшое время) находить коллизии.

В 2005 году Ван Сяоюнь и Юй Хунбо из университета Шаньдун в Китае опубликовали алгоритм, который может найти две различные последовательности в 128 байт, которые дают одинаковый MD5-хеш. Одна из таких пар:

и

Каждый из этих блоков даёт MD5-хеш, равный 79054025255fb1a26e4bc422aef54eb4.

Метод Ван Сяоюня и Юй Хунбо

Метод Ван Сяоюня и Юй Хунбо использует тот факт, что MD5 построен на итерационном методе Меркла-Дамгарда. Поданный на вход файл сначала дополняется, так чтобы его длина была кратна 64 байтам, после этого он делится на блоки по 64 байта каждый M₀,M₁,…,M_n-1. Далее вычисляется последовательность 16-байтных состояний s₀,…,s_n по правилу s_i+1=f, где f некоторая фиксированная функция. Начальное состояние s₀ называется инициализирующим вектором.

Метод позволяет для заданного инициализирующего вектора найти две пары M,M' и N,N', такие что f,M') = f,N'). Важно отметить, что этот метод работает для любого инициализирующего вектора, а не только для вектора используемого по стандарту.

Эта атака является разновидностью дифференциальной атаки, которая, в отличие от других атак этого типа, использует целочисленное вычитание а не XOR в качестве меры разности. При поиске коллизий используется метод модификации сообщений: сначала выбирается произвольное сообщение M₀, далее оно модифицируется по некоторым правилам, сформулированным в статье, после чего вычисляется дифференциал хеш-функции, причём M'₀ = M₀ + dM₀ с вероятностью 2. К M₀ и M'₀ применяется функция сжатия для проверки условий коллизии; далее выбирается произвольное M₁, модифицируется, вычисляется новый дифференциал, равный нулю с вероятностью 2, а равенство нулю дифференциала хеш-функции как раз означает наличие коллизии. Оказалось, что найдя одну пару M₀ и M'₀, можно менять лишь два последних слова в M₀, тогда для нахождения новой пары M₁ и M'₁ требуется всего около 2 операций хеширования.

Применение этой атаки к MD4 позволяет найти коллизию меньше чем за секунду. Она также применима к другим хеш-функциям, таким как RIPEMD и HAVAL.

В 2006 году чешский исследователь Властимил Клима опубликовал алгоритм, позволяющий находить коллизии на обычном компьютере с любым начальным вектором при помощи метода, названного им «туннелирование».