Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Лямбда-исчисление - Каррирование23 января 2011Оглавление: 1. Лямбда-исчисление 2. Чистое 3. 4. Каррирование 5. Связь с рекурсивными функциями 6. В языках программирования Функция двух переменных x и y f = x + y может быть рассмотрена как функция одной переменной x, возвращающая функцию одной переменной y, то есть как выражение Семантика бестипового λ-исчисленияТот факт, что термы λ-исчисления действуют как функции, применяемые к термам λ-исчисления, приводит к сложностям построения адекватной семантики λ-исчисления. Можно ли приписать λ-исчислению какой-либо смысл? Желательно иметь множество D, в которое вкладывалось бы его пространство функций D → D. В общем случае такого D не существует по соображениям ограничений на мощности этих двух множеств, D и функций из D в D: второе имеет большую мощность, чем первое. Эту трудность преодолел Д. С. Скотт, построив понятие области D и урезав D → D до непрерывных функций. После этого также стало понятно, как можно строить денотационную семантику языков программирования. Это произошло благодаря тому, что с помощью конструкций Скотта можно придать значение также двум важным конструкциям языков программирования — рекурсии и типам данных. Для множества D, которое было бы изоморфно его пространству функций D → D, имеются модели лямбда-исчисления в теории множеств с самопринадлежностью, доказательство непоротиворечивости лямбда-исчисления в этом случае, в семантике самопринадлежности, отличается краткостью, см.. Просмотров: 5250
|
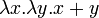 . Такой приём работает точно так же для функций любой арности. Это показывает, что функции многих переменных могут быть без проблем выражены в λ-исчислении и являются «синтаксическим сахаром». Описанный процесс превращения функций многих переменных в функцию одной переменной называется карринг, в честь американского математика Хаскелла Карри, хотя первым его предложил М. И. Шейнфинкель.
. Такой приём работает точно так же для функций любой арности. Это показывает, что функции многих переменных могут быть без проблем выражены в λ-исчислении и являются «синтаксическим сахаром». Описанный процесс превращения функций многих переменных в функцию одной переменной называется карринг, в честь американского математика Хаскелла Карри, хотя первым его предложил М. И. Шейнфинкель.