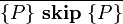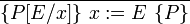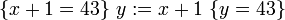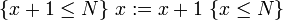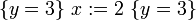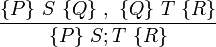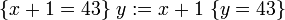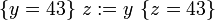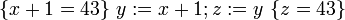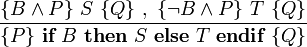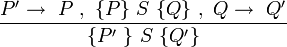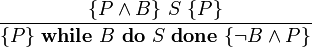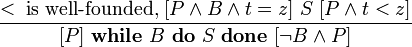Логика Хоара - Частичная и полная корректность

Интернет магазин китайских планшетных компьютеров

Компьютеры - Логика Хоара - Частичная и полная корректность

23 января 2011

Оглавление:
1. Логика Хоара
2. Частичная и полная корректность
3. Примеры

В стандартной логике Хоара может быть доказана только частичная корректность, так как завершение программы нужно доказывать отдельно. Таким образом, «интуитивное» понимание тройки Хоара можно выразить так: если P имеет место до выполнения C, то либо имеет место Q, либо C никогда не завершится. Действительно, если C не завершается, никакого «после» нет, поэтому Q может быть любым утверждением. Более того, мы можем выбрать Q со значением «ложь», чтобы показать, что C никогда не завершится.

Полная корректность также может быть доказана с использованием расширенной версии правила для оператора While.

Правила

Аксиома пустого оператора

Правило для пустого оператора утверждает, что оператор skip не меняет состояния программы, поэтому утверждение, верное до skip, остаётся верным после его выполнения.

$\frac{}{\{P\}\ \textbf{skip}\ \{P\}} \!$

Аксиома оператора присваивания

Аксиома оператора присваивания утверждает, что после присваивания, значение любого предиката относительно правой части присваивания не меняется с заменой правой на левую часть:

$\frac{}{\{P\}\ x:=E \ \{P\} } \!$

Здесь P означает выражение P в котором все вхождения свободной переменной x заменены выражением E.

Смысл аксиомы присваивания заключается в том, что истинность {P} эквивалентна {P} после выполнения присваивания. Таким образом, если {P} имело значение «истина» до присваивания, согласно аксиоме присваивания {P} будет иметь значение «истина» после присваивания. И наоборот, если {P} было равно «ложь» до оператора присваивания, {P} должно быть равно «ложь» после.

Примеры корректных троек:

$\{x + 1 = 43\}\ y := x + 1\ \{ y = 43 \}\!$
$\{x + 1 \leq N \}\ x := x + 1\ \{x \leq N\}\ \!$

Аксиома присваивания в формулировке Хоара не применима, когда более одного идентификатора ссылаются на одно и то же значение. Например,

$\{ y = 3\} \ x := 2\ \{y = 3 \}$

является неверным утверждением, если x и y ссылаются на одну и ту же переменную, так как никакое предусловие не может обеспечить, чтобы y было равно 3 после того, как x присвоено 2.

Правило композиции

Правило композиции Хоара применяется к последовательному выполнению программ S и T, где S выполняется до T, что записывается как S;T.

$\frac {\{P\}\ S\ \{Q\}\ , \ \{Q\}\ T\ \{R\} } {\{P\}\ S;T\ \{R\}} \!$

Например, рассмотрим два экземпляра аксиомы присваивания:

$\{ x + 1 = 43\} \ y := x + 1\ \{y =43 \}$

$\{ y = 43\} \ z := y\ \{z = 43 \}$

Согласно правилу композиции, мы получаем:

$\{ x + 1 = 43\} \ y:=x + 1; z:= y\ \{z =43 \}$

Правило условного оператора

$\frac { \{B \wedge P\}\ S\ \{Q\}\ ,\ \{\neg B \wedge P \}\ T\ \{Q\} } { \{P\}\ \textbf{if}\ B\ \textbf{then}\ S\ \textbf{else}\ T\ \textbf{endif}\ \{Q\} } \!$

Правило вывода

$\frac { P^\prime \rightarrow\ P\ ,\ \lbrace P \rbrace\ S\ \lbrace Q \rbrace\ ,\ Q \rightarrow\ Q^\prime } { \lbrace P^\prime\ \rbrace\ S\ \lbrace Q^\prime\rbrace } \!$

Правило оператора цикла

$\frac { \{P \wedge B \}\ S\ \{P\} } { \{P \}\ \textbf{while}\ B\ \textbf{do}\ S\ \textbf{done}\ \{\neg B \wedge P\} } \!$

Здесь P является инвариантом цикла.

Правило оператора цикла с полной корректностью

$\frac { <\;\textrm{is\ well-founded,}\;\ S\} {\ \textbf{while}\ B\ \textbf{do}\ S\ \textbf{done}\ } \!$

В этом правиле, кроме сохранения инварианта цикла, доказывается завершение цикла при помощи терма, называемого переменной цикла, значение которого строго уменьшается согласно отношения полной фундированности "<" с каждой итерацией. При этом условие B должно подразумевать, что t не является минимальным элементом своей области определения, в противном случае посылка данного правила будет ложной. Поскольку отношение "<" является полностью фундированным, каждый шаг цикла определяется уменьшающимися членами конечного линейно упорядоченного множества.

В записи данного правила используются квадратные, а не фигурные скобки, для того чтобы обозначить полную корректность правила.

<<< Логика в информатике

Лямбда-исчисление >>>

Компьютерное аппаратное обеспечение
Вычислительные комплексы
Компьютерные данные
Компьютерные журналы
Классы компьютеров
Компьютеры

Программное обеспечение
Производители компьютеров
Профессии в ИТ
Системное администрирование
Компьютерный сленг
Списки компьютерных терминов

Человеко-компьютерное взаимодействие