Интернет магазин китайских планшетных компьютеров |
||
Компьютеры - Логические элементы - Двоичные логические операции с цифровыми сигналами22 января 2011Оглавление: 1. Логические элементы 2. Двоичные логические операции с цифровыми сигналами 3. Физические реализации логических элементов 4. Применение логических элементов Логические операции своё теоретическое обоснование получили в алгебре логики. Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными и т. д. Из Отрицание, НЕТ, НЕ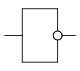
Инвертор, НЕ
Мнемоническое правило для отрицания звучит так: На выходе будет:
Повторение, ДА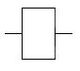
Повторитель ДА
Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками. Из Конъюнкция. Операция 2И. Функция min
2И
Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
Дизъюнкция. Операция 2ИЛИ. Функция max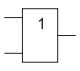
2ИЛИ
Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
Инверсия функции конъюнкции. Операция 2И-НЕ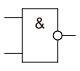
2И-НЕ
Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:
Инверсия функции дизъюнкции. Операция 2ИЛИ-НЕ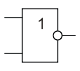
2ИЛИ-НЕ
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:
Эквивалентность, 2ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕXNOR gate http://imageshack.us/photo/my-images/151/xnorimg.png/
Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:
Сложение по модулю 2. Инверсия равнозначности.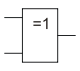
В англоязычной литературе 2XOR.
Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:
Импликация от A к B
Мнемоническое правило для инверсии декремента звучит так: На выходе будет:
Импликация от B к A
Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:
Декремент. Запрет импликации по B. Инверсия импликации от A к B
Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:
Инкремент. Запрет импликации по A. Инверсия импликации от B к A
Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:
Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2. Этими простейшими логическими операциями, и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:
Для преобразования логических функций в один из названых базисов необходимо применять Закон де-Моргана. Просмотров: 5860
|
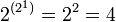 возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.
возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.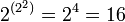 возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.
возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.