Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Линейное программирование - Математическая формулировка23 января 2011Оглавление: 1. Линейное программирование 2. Математическая формулировка 3. Алгоритмы решения 4. История Нужно определить максимум линейной целевой функции при условиях
Иногда на xi также накладывается некоторый набор ограничений в виде равенств, но от них можно избавиться, последовательно выражая одну переменную через другие и подставляя её во всех остальных равенствах и неравенствах. Такую задачу называют «основной» или «стандартной» в линейном программировании. Примеры задачМаксимальное паросочетаниеРассмотрим задачу о максимальном паросочетании в двудольном графе: есть несколько юношей и девушек, причём для каждых юноши и девушки известно, симпатичны ли они друг другу. Нужно поженить максимальное число пар со взаимной симпатией. Введём переменные xij, которые соответствуют паре из i-того юноши и j-той девушки и удовлетворяют ограничениям: с целевой функцией Максимальный потокПусть имеется граф, в котором для каждого ребра указана его пропускная способность. И заданы две вершины: сток и исток. Нужно указать для каждого ребра, сколько через него будет протекать жидкости так, чтобы максимизировать суммарный поток из истока в сток. Возьмём в качестве переменных xi — количество жидкости, протекающих через i-тое ребро. Тогда
где ci — пропускная способность i-того ребра. Эти неравенства надо дополнить равенством количества втекающей и вытекающей жидкости для каждой вершины, кроме стока и истока. В качестве функции f естественно взять разность между количеством вытекающей и втекающей жидкости в истоке. Обобщение предыдущей задачи — максимальный поток минимальной стоимости. В этой задаче даны стоимости для каждого ребра и нужно среди максимальных потоков выбрать поток с минимальной стоимостью. Эта задача сводится к двум задачам линейного программирования: сначала нужно решить задачу о максимальном потоке, а потом добавить к этой задаче ограничение Эти задачи могут быть решены быстрее, чем общими алгоритмами решения задач линейного программирования, за счёт особой структуры уравнений и неравенств. Транспортная задачаИмеется некий однородный груз, который нужно перевести с n складов на m заводов. Для каждого склада i известно, сколько в нём находится груза ai, а для каждого завода известна его потребность bj в грузе. Стоимость перевозки пропорциональна расстоянию от склада до завода. Требуется составить наиболее дешёвый план перевозки. Решающими переменными в данном случае являются xij — количества груза, перевезённого из i-го склада на j-й завод. Они удовлетворяют ограничениям: Целевая функция имеет вид: Игра с нулевой суммойЕсть матрица A размера Пусть в оптимальной стратегии, например, первого игрока число i нужно выбирать с вероятностью pi. Тогда оптимальная стратегия является решением следующей задачи линейного программирования:
в которой нужно максимизировать функцию Просмотров: 3810
|
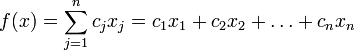
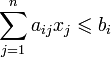 при
при 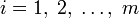 .
.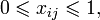
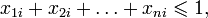
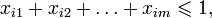
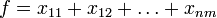 . Можно показать, что среди оптимальных решений этой задачи найдётся целочисленное. Переменные, равные 1, будут соответствовать парам, которые следует поженить.
. Можно показать, что среди оптимальных решений этой задачи найдётся целочисленное. Переменные, равные 1, будут соответствовать парам, которые следует поженить.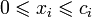 ,
,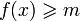 , где m — величина максимального потока, и решить задачу с новой функцией f — стоимостью потока.
, где m — величина максимального потока, и решить задачу с новой функцией f — стоимостью потока.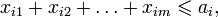
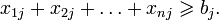
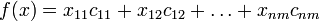 , которую надо минимизировать.
, которую надо минимизировать.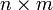 . Первый игрок выбирает число от 1 до n, второй — от 1 до m. Затем они сверяют числа и первый игрок получает aij очков, а второй очков. Нужно найти оптимальную стратегию первого игрока.
. Первый игрок выбирает число от 1 до n, второй — от 1 до m. Затем они сверяют числа и первый игрок получает aij очков, а второй очков. Нужно найти оптимальную стратегию первого игрока.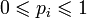 ,
,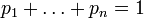 ,
,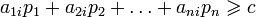 ,
,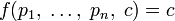 . Значение c в оптимальном решении будет математическим ожиданием выигрыша первого игрока в наихудшем случае.
. Значение c в оптимальном решении будет математическим ожиданием выигрыша первого игрока в наихудшем случае.