Интернет магазин китайских планшетных компьютеров |
|||
Компьютеры - Квантовый компьютер - Теория22 января 2011Оглавление: 1. Квантовый компьютер 2. Теория 3. Применение квантовых компьютеров 4. Физические реализации квантовых компьютеров 5. Пример реализации операции CNOT на зарядовых состояниях электрона в квантовых точках КубитыИдея квантовых вычислений, впервые высказанная Ю. И. Маниным и Р. Фейнманом, состоит в том, что квантовая система из L двухуровневых квантовых элементов имеет 2 линейно независимых состояний, а значит, вследствие принципа квантовой суперпозиции, пространством состояний такого квантового регистра является 2-мерное гильбертово пространство. Операция в квантовых вычислениях соответствует повороту вектора состояния регистра в этом пространстве. Таким образом, квантовое вычислительное устройство размером L кубит фактически задействует одновременно 2 классических состояний. Физическими системами, реализующими кубиты, могут быть любые объекты, имеющие два квантовых состояния: поляризационные состояния фотонов, электронные состояния изолированных атомов или ионов, спиновые состояния ядер атомов, и т.д. Один классический бит может находиться в одном и только в одном из состояний Пример:
Приведем для объяснения два примера из квантовой механики: 1) фотон находится в состоянии Перейдем к системе из двух кубитов. Измерение каждого из них может дать 0 или 1. Поэтому у системы есть 4 классических состояния: 00, 01, 10 и 11. Аналогичные им базовые квантовые состояния: Если мы измерим только первый кубит квантовой системы, находящейся в состоянии
В первом случае измерение даст состояние Мы снова видим, что результат такого измерения невозможно записать как вектор в гильбертовом пространстве состояний. Такое состояние, в котором участвует наше незнание о том, какой же результат получится на первом кубите, называют смешанным состоянием. В нашем случае такое смешанное состояние называют проекцией исходного состояния В общем случае системы из L кубитов, у неё 2 классических состояний, …00001, … , 11111…), каждое из которых может быть измерено с вероятностями 0—100 %. Таким образом, одна операция над группой кубитов затрагивает все значения, которые она может принимать, в отличие от классического бита. Это и обеспечивает беспрецедентный параллелизм вычислений. ВычислениеУпрощённая схема вычисления на квантовом компьютере выглядит так: берется система кубитов, на которой записывается начальное состояние. Затем состояние системы или её подсистем изменяется посредством унитарных преобразований, выполняющих те или иные логические операции. В конце измеряется значение, и это результат работы компьютера. Роль проводов классического компьютера играют кубиты, а роль логических блоков классического компьютера играют унитарные преобразования. Такая концепция квантового процессора и квантовых логических вентилей была предложена в 1989 году Д. Дейчем. Также Д. Дейч в 1995 году нашёл универсальный логический блок, с помощью которого можно выполнять любые квантовые вычисления. Оказывается, что для построения любого вычисления достаточно двух базовых операций. Квантовая система дает результат, только с некоторой вероятностью являющийся правильным. Но за счет небольшого увеличения операций в алгоритме можно сколь угодно приблизить вероятность получения правильного результата к единице. С помощью базовых квантовых операций можно симулировать работу обычных логических элементов, из которых сделаны обычные компьютеры. Поэтому любую задачу, которая решена сейчас, квантовый компьютер решит, и почти за такое же время. Следовательно, новая схема вычислений будет не слабее нынешней. Чем же квантовый компьютер лучше классического? Большая часть современных ЭВМ работают по такой же схеме: n бит памяти хранят состояние и каждый такт времени изменяются процессором. В квантовом случае система из n кубитов находится в состоянии, являющимся суперпозицией всех базовых состояний, поэтому изменение системы касается всех 2 базовых состояний одновременно. Теоретически новая схема может работать намного быстрее классической. Практически алгоритм Гровера поиска в базе данных показывает квадратичный прирост мощности против классических алгоритмов Алгоритмы
Было показано, что не для всякого алгоритма возможно «квантовое ускорение». Более того, возможность получения квантового ускорения для произвольного классического алгоритма является большой редкостью . Квантовая телепортацияАлгоритм телепортации реализует точный перенос состояния одного кубита на другой. В простейшей схеме используются 4 кубита: источник, приёмник и два вспомогательных. Отметим, что в результате работы алгоритма первоначальное состояние источника разрушится — это пример действия общего принципа невозможности клонирования — невозможно создать точную копию квантового состояния, не разрушив оригинал. На самом деле, довольно легко создать одинаковые состояния на кубитах. К примеру, измерив 3 кубита, мы переведем каждый из них в базовые состояния и хотя бы на двух из них они совпадут. Не получится скопировать произвольное состояние, и телепортация — замена этой операции. Телепортация позволяет передавать квантовое состояние системы с помощью обычных классических каналов связи. Таким образом, можно, в частности, получить связанное состояние системы, состоящей из подсистем, удаленных на большое расстояние. Просмотров: 6560
|
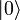 или
или 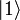 . Квантовый бит, называемый кубитом, находится в состоянии
. Квантовый бит, называемый кубитом, находится в состоянии 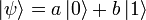 , так что |a|² и |b|² — вероятности получить 0 или 1 соответственно при измерении этого состояния;
, так что |a|² и |b|² — вероятности получить 0 или 1 соответственно при измерении этого состояния; 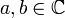 ; |a|² + |b|² = 1. Сразу после измерения кубит переходит в базовое квантовое состояние, соответствующее классическому результату.
; |a|² + |b|² = 1. Сразу после измерения кубит переходит в базовое квантовое состояние, соответствующее классическому результату.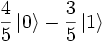
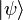 суперпозиции двух поляризаций. Это состояние есть вектор в двумерной плоскости, систему координат в которой можно представлять как две перпендикулярные оси, так что a и b есть проекции
суперпозиции двух поляризаций. Это состояние есть вектор в двумерной плоскости, систему координат в которой можно представлять как две перпендикулярные оси, так что a и b есть проекции 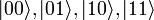 . И наконец, общее квантовое состояние системы имеет вид
. И наконец, общее квантовое состояние системы имеет вид 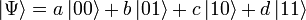 . Теперь |a|² — вероятность измерить 00 и т. д. Отметим, что |a|²+|b|²+|c|²+|d|²=1 как полная вероятность.
. Теперь |a|² — вероятность измерить 00 и т. д. Отметим, что |a|²+|b|²+|c|²+|d|²=1 как полная вероятность.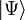 , у нас получится:
, у нас получится: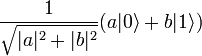 , а
, а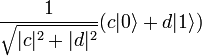 .
.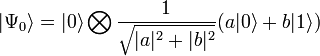 , во втором — состояние
, во втором — состояние 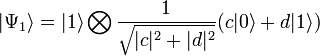
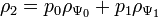 где матрица плотности состояния
где матрица плотности состояния 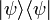 .
.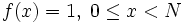 за время
за время 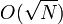 .
.