Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Квантовая логика23 января 2011раздел логики, необходимый для рассуждения о предложениях, которые учитывают принципы квантовой теории. Эта область исследований была основана в 1936 году работой Гарита Бирхофа и Джона фон Неймана, которые пытались примирить очевидную несогласованность классической логики с фактами по поводу измерения дополнительных переменных в квантовой механике, как например координата и импульс. Квантовая логика может быть сформулирована как измененная версия логики высказываний. Она имеет несколько свойств, которые отличают её от классической логики. В частности, отсутствие дистрибутивности:
где символы p, q и r — логические переменные. Чтобы проиллюстрировать, почему дистрибутивный закон не работает, рассмотрим движущуюся по прямой частицу. Далее, пусть логические переменные p, q и r имеют следующие значения:
Тогда предложение «
С другой стороны, «
и дистрибутивность не может существовать. Представьте лабораторию, которая имеет аппаратуру, необходимую для измерения скорости пули, выпущеной из огнестрельного оружия. Тщательно подбирая условия, необходимо неоднократно выстрелить из одного и того же оружия и провести измерения скоростей. Это даст некоторое распределение скоростей. Однако мы не будем стремиться получить тем же образом эти значения для каждого индивидуального измерения, для каждой группы измерений; мы ожидаем, что эксперимент приводит к такому же распределению скоростей. В частности, мы можем ожидать распределения вероятностей предложениям, например, { a ≤ скорость ≤ b}. Поэтому естественно предложить, что при контролируемых условиях подготовки измерение классической системы можно описать мерой вероятности на пространстве состояний. Такая же статистическая структура также присутствует в квантовой механике. Мера квантовой вероятности функция P определяется на Q со значениями в таком, что P =0, P =1 и если {Ei}i — последовательность парами ортогональных элементов Q, тогда справедлива следующая теорема: Теорема Эндрю Глизона: Пусть H — отделимое комплексное Гильбертово пространство, как минимум размерности 3. Оператор S не обязательно отрицателен и следа 1. Такой оператор часто называется оператором плотности. Физики обычно представляют оператор плотности, как матрица плотности относительно некоторого ортонормального базиса. Для более подробной информации о статистике квантовых систем, смотрите квантовую статистическую механику. Просмотров: 1273
|
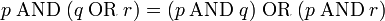 ,
,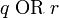 » всегда верно, точно как и
» всегда верно, точно как и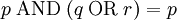
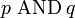 » и «
» и «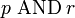 » неверны, так как требуют более жёстких условий одновременных значений позиции и инерции, что не возможно по принципу неопределённости Гейзенберга. Поэтому
» неверны, так как требуют более жёстких условий одновременных значений позиции и инерции, что не возможно по принципу неопределённости Гейзенберга. Поэтому